Задания по теме «Многогранник»

Ребро D_2D перпендикулярно плоскости ABCD, поэтому угол D_2DB — прямой. Тогда tg \angle D_2BD =\frac{D_2D}{DB}. По теореме Пифагора (DB)^2 = (AD)^2 + (AB)^2 = 16 + 16 = 32. DB = 4\sqrt2. Отсюда, tg \angle D_2BD =\frac{4}{4\sqrt2}=\frac{1}{\sqrt2}, (tg\angle D_2BD)^2=\frac12=0,5.

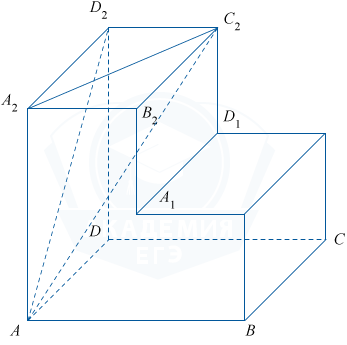
Ребро C_2D_2 перпендикулярно плоскости AA_2D_2D, поэтому угол C_2D_2A — прямой. По теореме Пифагора (AC_2)^2 =  (AD_2)^2 +(D_2C_2)^2. (AD_2)^2 =  (AD)^2 +(DD_2)^2 =  4^2 + 4^2 =  32. Отсюда, (AC_2)^2 = 32 + 2^2 = 36,  AC_2 = 6.

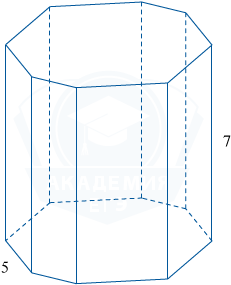
Площадь боковой поверхности призмы находим по формуле S_бок. = P_осн. · h = 8a\cdot h, где P_осн. и h — соответственно периметр основания и высота призмы, равная 7, и a — сторона правильного восьмиугольника, равная 5. Следовательно, S_бок. = 8\cdot 5\cdot 7 = 280.

Указанный в условии многогранник является треугольной пирамидой, в основании которой лежит треугольник ABC, а высотой является боковое ребро призмы BB_1 так как BB_1\perp ABCD.

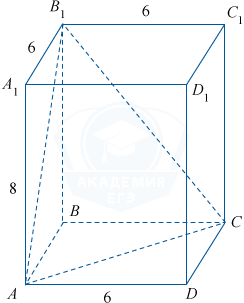
S_{ABC}= \frac12S_{ABCD}= \frac12\cdot AB\cdot BC= \frac12\cdot6\cdot6=18.

Отсюда, V_{ABCB_1}= \frac12S_{ABC}\cdot BB_1= \frac13S_{ABC}\cdot AA_1= \frac13\cdot18\cdot8= 48.

Данный многогранник является прямой призмой и получается объединением двух прямых призм. В основании первой призмы лежит прямоугольник со сторонами 3 и 3, а её высота h_1 равна 5. Объём этой призмы V_1 находим по формуле V₁ = S_осн. · h₁ = 3\cdot3\cdot5 = 45. В основании второй призмы лежит прямоугольник со сторонами 2 и 1, а её высота h_2 равна 5. Объём этой призмы V_2 находим по формуле V₂ = S_осн. · h₂ = 2\cdot1\cdot5 = 10. Объём V данного многогранника равен сумме объёмов указанных призм: V = V_1 + V_2 = 45 + 10 = 55.

Площадь поверхности S многогранника состоит из площади оснований и площади боковой поверхности. Площадь одного из двух равных оснований равна разности площадей двух прямоугольников, имеющих измерения 6×4 и 1×2, то есть 6\cdot4-2\cdot1. Площадь боковой поверхности равна произведению периметра основания многогранника на его высоту. Отсюда, S = 2 · S_осн. + S_бок. = 2 · S_осн. + P_осн. · h, где S_осн. P_осн. и h соответственно — площадь основания, периметр основания и высота многогранника. S=(6\cdot4-2\cdot1)\cdot2+ (2+1+1+6+4+6+1+1)\cdot4= 132.

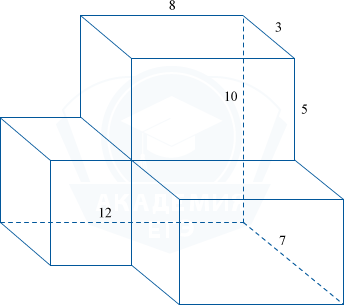
Данный многогранник состоит из четырех многогранников.

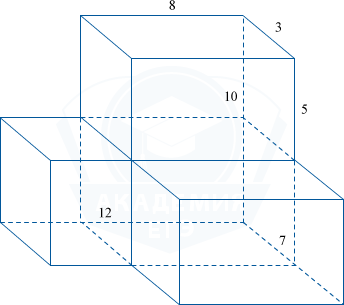
Объем данного многогранника состоит из суммы объемов четырех многогранников: V=V_1+V_2+V_3+V_4.

Измерения первого многогранника: 12-8=4;\;3;\;10-5=5.

Измерения второго многогранника: 8;\;3;\;5.

Измерения третьего многогранника: 8;\;4;\;5.

Измерения четвертого многогранника: 8;\;3;\;5.

Отсюда V=4\cdot3\cdot5+8\cdot3\cdot5+8\cdot4\cdot5+ 8\cdot3\cdot5= 60+120+160+120= 460.

Рассмотрим рисунок:

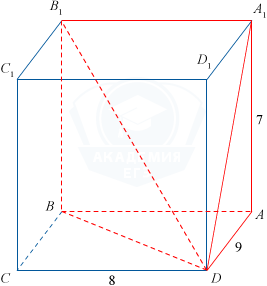
Многогранник DAA_1B_1B является пирамидой, в основании которой лежит прямоугольник AA_1B_1B, а высотой является AD.

Поэтому V_{DAA_1B_1B}= \frac13 S_{DAA_1B_1B}\cdot AD= \frac13\cdot7\cdot8\cdot9= 168.

Для вычисления объема многогранника DEFD_1E_1F_1 воспользуемся формулой:

V = S \cdot h

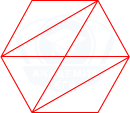
Так как в основании лежит правильный шестигранник, то площадь полученного треугольника DEF равна \frac16 от площади шестигранника (см. рис.). Соответственно объем многогранника равен:

V = \frac16 \cdot 10 \cdot h = \frac53 \cdot 12 = 20

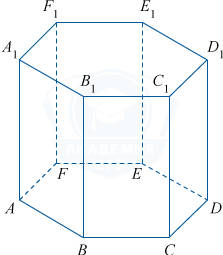
Объем многогранника ABCA_1B_1C_1 можно вычислить по формуле:

V = S \cdot h

Площадь образованного треугольника ABC равна \frac16 от площади основания призмы (см. рис.). Соответственно объем многогранника равен:

V = \frac16 \cdot 12 \cdot h = \frac16 \cdot 12 \cdot 5 = 10