Задание №1073

Тип задания: 8
Тема: Комбинации геометрических фигур

Условие

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 24. Найдите площадь поверхности шара.

Шар вписанный в цилиндр

Показать решение

Решение

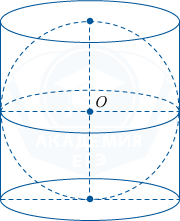
Из рисунка, указанного в условии, видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим площадь полной поверхности цилиндра: S _{полн. пов. цил.} = 2S _{осн. цил.} + S _{бок. пов. цил.} = 2\pi R^2 + 2\pi RH.

2\pi R^2 + 2\pi RH = 2\pi R^2 + 2\pi R\cdot 2R = 6\pi R^2. По условию 24 = 6\pi R^2. Отсюда \pi R^2 = 4. Так как S _{пов. шара} = 4\pi R^2, то искомая площадь равна 4\cdot 4 = 16.