Задания по теме «Угол между плоскостями»

а) В \triangle DCN и \triangle MAD имеем: \angle C=\angle A=90^{\circ}, CN=AM=\frac12AB, CD=DA.

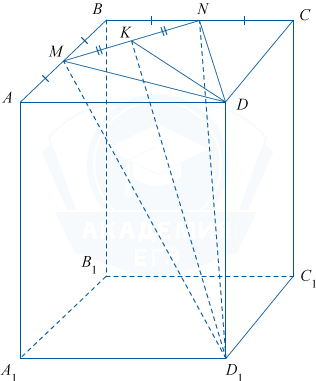
Отсюда \triangle DCN=\triangle MAD по двум катетам. Тогда MD=DN, \triangle DMN равнобедренный. Значит, медиана DK — является также высотой. Следовательно, DK \perp MN.

DD_1 \perp MND по условию, D_1K — наклонная, KD — проекция, DK \perp MN.

Отсюда по теореме о трех перпендикулярах MN\perp D_1K.

б) Как было доказано в а), DK \perp MN и MN \perp D_1K, но MN — линия пересечения плоскостей MND_1 и ABC, значит \angle DKD_1 — линейный угол двугранного угла между плоскостями MND_1 и ABC.

В \triangle DAM по теореме Пифагора DM= \sqrt {DA^2+AM^2}= \sqrt {64+16}= 4\sqrt 5, MN= \sqrt {MB^2+BN^2}= \sqrt {16+16}= 4\sqrt 2. Следовательно, в \triangle DKM по теореме Пифагора DK= \sqrt {DM^2-KM^2}= \sqrt {80-8}= 6\sqrt 2. Тогда в \triangle DKD_1, tg\angle DKD_1=\frac{DD_1}{DK}=\frac{6\sqrt 2}{6\sqrt 2}=1.

Значит, \angle DKD_1=45^{\circ}.

45^{\circ}.

а) Плоскость AMN пересекает ребро DD_1 в точке K, являющейся четвёртой вершиной сечения данной призмы этой плоскостью. Сечением является параллелограмм ANMK, потому что противоположные грани данной призмы параллельны.

BN =\frac13BB_1=2. Проведём KL \parallel CD, тогда треугольники ABN и KLM равны, значит ML=BN=2, LC=MC-ML=3-2=1, KD=LC=1. Тогда KD_1=6-1=5. Теперь можно найти отношение KD:KD_1=1:5.

б) F — точка пересечения прямых CD и KM. Плоскости ABC и AMN пересекаются по прямой AF. Угол \angle KHD =\alpha — линейный угол двугранного угла (HD\perp AF, тогда по теореме, обратной теореме о трех перпендикулярах, KH \perp AF), и является острым углом прямоугольного треугольника KHD, катет KD=1.

Треугольники FKD и FMC подобны (KD \parallel MC), поэтому FD:FC=KD:MC, решая пропорцию FD:(FD+4)=1:3, получим FD=2. В прямоугольном треугольнике AFD (\angle D=90^{\circ}) с катетами 2 и 4 вычислим гипотенузу AF=\sqrt {4^2+2^2}=2\sqrt 5, DH= AD\cdot FD:AF= \frac{4\cdot 2}{2\sqrt 5}= \frac4{\sqrt 5}.

В прямоугольном треугольнике KHD найдём tg \alpha =\frac{KD}{DH}=\frac{\sqrt 5}4, значит, искомый угол \alpha =arctg\frac{\sqrt 5}4.

а) 1:5;

б) arctg\frac{\sqrt 5}4.

а) Пусть KO — высота пирамиды, F — середина MK; FE \parallel MP (в плоскости PKM ). Так как FE — средняя линия \triangle PKM, то FE=\frac{MP}2.

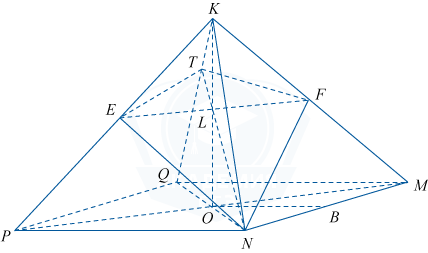
Построим сечение пирамиды плоскостью, проходящей через NF и параллельной MP, то есть плоскостью NFE. L — точка пересечения EF и KO. Так как точки L и N принадлежат искомому сечению и лежат в плоскости KQN, то точка T, полученная как пересечение LN и KQ, является также точкой пересечения искомого сечения и ребра KQ. NETF — искомое сечение.

б) Плоскости NFE и MPK пересекаются по прямой FE. Значит, угол между этими плоскостями равен линейному углу двугранного угла OFEN, построим его: LO \perp MP, MP \parallel FE, следовательно, LO \perp FE; \triangle NFE — равнобедренный (NE=NF как соответствующие медианы равных треугольников KPN и KMN ), NL — его медиана (EL=LF, так как PO=OM, а \triangle KEF \sim \triangle KPM ). Отсюда NL \perp FE и \angle NLO — искомый.

ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.

\triangle KON — прямоугольный.

Катет KO по теореме Пифагора равен KO=\sqrt {KN^2-ON^2}.

OL= \frac12KO= \frac12\sqrt{KN^2-ON^2}= \frac12\sqrt {9\cdot 26-9\cdot 2}= \frac12\sqrt{9(26-2)}= \frac32\sqrt {24}= \frac32\cdot 2\sqrt 6= 3\sqrt 6.

tg\angle NLO =\frac{ON}{OL}=\frac{3\sqrt 2}{3\sqrt 6}=\frac1{\sqrt 3},

\angle NLO=30^{\circ}.

30

а) Пусть D и E — середины ребер AC и BB_{1} соответственно.

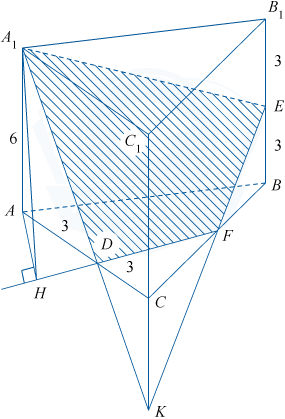
В плоскости AA_{1}C_{1} проведем прямую A_{1}D, которая пересекает прямую CC_{1} в точке K, в плоскости BB_{1}C_{1} — прямую KE, которая пересекает ребро BC в точке F. Соединие точки A_{1} и E, лежащие в плоскости AA_{1}B_{1}, а также D и F, лежащие в плоскости ABC, получим сечение A_{1}EFD.

\bigtriangleup AA_{1}D=\bigtriangleup CDK по катету AD=DC и острому углу.

\angle ADA_{1}=\angle CDK — как вертиальные, отсюда следует, что AA_{1}=CK=6. \bigtriangleup CKF и \bigtriangleup BFE подобны по двум углам \angle FBE=\angle KCF=90^\circ, \angle BFE=\angle CFK — как вертикальные.

\frac{CK}{BE}=\frac{6}{3}=2, то есть коэффициент подобия равен 2, откуда следует, что CF:FB=2:1.

б) Проведём AH \perp DF. Угол между плоскостью сечения и плоскостью основания равен углу AHA_{1}. Действительно, отрезок AH \perp DF (DF — линия пересечения этих плоскостей) и является проекцией отрезка A_{1}H на плоскость основания, следовательно, по теореме о трёх перпендикулярах, A_{1}H \perp DF. \angle AHA_{1}=arctg\frac{AA_{1}}{AH}. AA_{1}=6.

Найдём AH. \angle ADH =\angle FDC (как вертикальные).

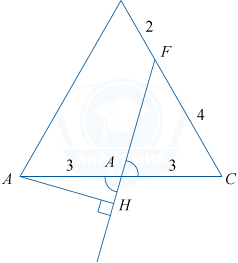
По теореме косинусов в \bigtriangleup DFC:

DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac{1}{2}=13.

FC^2=DF^2+DC^2- 2DF \cdot DC \cdot \cos \angle FDC,

4^2=13+9-2\sqrt{13} \cdot 3 \cdot \cos \angle FDC,

\cos \angle FDC=\frac{6}{2\sqrt{13} \cdot 3}=\frac{1}{\sqrt{13}}.

По следствию из основного тригонометрического тождества

\sin \angle FDC=\sqrt{1-\left ( \frac{1}{\sqrt{13}}\right )^2}=\frac{2\sqrt{3}}{\sqrt{13}}. Из \bigtriangleup ADH найдём AH:

AH=AD \cdot \sin \angle ADH, (\angle FDC=\angle ADH). AH=3 \cdot \frac{2\sqrt{3}}{\sqrt{13}}=\frac{6\sqrt{13}}{\sqrt{13}}.

\angle AHA_{1}= arctg\frac{AA_{1}}{AH}= arctg\frac{6 \cdot \sqrt{13}}{6\sqrt{3}}= arctg\frac{\sqrt{39}}{3}.

arctg\frac{\sqrt{39}}{3}.

а) Будем использовать метод координат. Найдём скалярное произведение векторов \vec{PK} и \vec{PB_{1}}, а затем косинус угла между этими векторами. Направим ось Oy вдоль CD, ось Oz вдоль CC_{1}, и ось Ox \perp CD. C — начало координат.

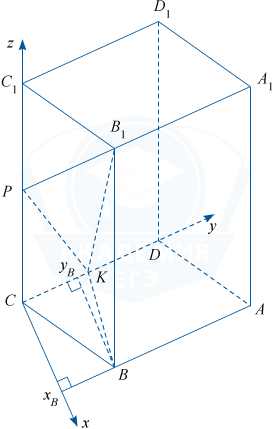
Тогда C (0;0;0); C_{1}(0;0;10); P(0;0;5); K(0;5;0); B(BC \cos 30^\circ; BC\sin 30^\circ; 0), то есть B(5\sqrt{3}; 5;0), B_{1}(5\sqrt{3}; 5;10).

Найдём координаты векторов: \vec{PK}=\{0;5;-5\}; \vec{PB_{1}}=\{5\sqrt{3}; 5;5\}.

Пусть угол между \vec{PK} и \vec{PB_{1}} равен \alpha.

Получаем \cos \alpha=\frac{\vec{PK} \cdot \vec{PB_{1}}}{|\vec{PK}| \cdot |\vec{PB_{1}}|}= \frac{0 \cdot 5\sqrt{3} + 5 \cdot 5-5 \cdot 5}{|\vec{PK}| \cdot |\vec{PB_{1}}|}=0.

\cos \alpha =0, значит, \vec{PK} \perp \vec{PB_{1}} и прямые PK и PB_{1} перпендикулярны.

б) Угол между плоскостями равен углу между ненулевыми векторами, перпендикулярными этим плоскостям (или, если угол тупой, смежному с ним углу). Такие векторы называют нормалями к плоскостям. Найдём их.

Пусть \vec{n_{1}}=\{x; y; z\} перпендикулярен плоскости PKB_{1}. Найдем его, решив систему \begin{cases} \vec{n_{1}} \perp \vec{PK}, \\ \vec{n_{1}} \perp \vec{PB_{1}}. \end{cases}

\begin{cases} \vec{n_{1}} \cdot \vec{PK}=0, \\ \vec{n_{1}} \cdot \vec{PB_{1}}=0; \end{cases}

\begin{cases} 0x+5y-5z=0, \\ 5\sqrt{3}x+5y+5z=0; \end{cases}

\begin{cases}y=z, \\ x=\frac{-y-z}{\sqrt{3}}. \end{cases}

Возьмем y=1; z=1; x=\frac{-2}{\sqrt{3}}, \vec{n_{1}}=\left \{ \frac{-2}{\sqrt{3}}; 1;1 \right \}.

Пусть \vec{n_{2}}=\{x; y; z\} перпендикулярен плоскости C_{1}B_{1}B. Найдем его, решив систему \begin{cases} \vec{n_{2}} \perp \vec{CC_{1}}, \\ \vec{n_{2}} \perp \vec{CB}. \end{cases}

\vec{CC_{1}}=\{0;0;10\}, \vec{CB}=\{5\sqrt{3}; 5; 0\}.

\begin{cases} \vec{n_{2}} \cdot \vec{CC_{1}}=0, \\ \vec{n_{2}} \cdot \vec{CB}=0; \end{cases}

\begin{cases} 0x+0y+10z=0, \\ 5\sqrt{3}x+5y+0z=0; \end{cases}

\begin{cases}z=0, \\ y=-\sqrt{3}x. \end{cases}

Возьмем x=1; y=-\sqrt{3}; z=0, \vec{n_{2}}=\{1; -\sqrt{3};0\}.

Найдем косинус искомого угла \beta (он равен модулю косинуса угла между \vec{n_{1}} и \vec{n_{2}}).

\cos \beta= \frac{|\vec{n_{1}} \cdot \vec{n_{2}}|}{|\vec{n_{1}}| \cdot |\vec{n_{2}}|}= \frac{\left |-\dfrac{2}{\sqrt{3}}\cdot 1+1 \cdot (-\sqrt{3})+1 \cdot 0 \right |}{\sqrt{\dfrac{4}{3}+1+1} \cdot \sqrt{1+3+0}}= \frac{\dfrac{5}{\sqrt{3}}}{2\sqrt{\dfrac{10}{3}}}= \frac{\sqrt{10}}{4}.

\cos \beta =\frac{\sqrt{10}}{4}, \beta=\arccos\frac{\sqrt{10}}{4}.

\arccos\frac{\sqrt{10}}{4}

а) По условию ABCDA_{1}B_{1}C_{1}D_{1} — правильная призма, это означает, что основание ABCD — квадрат и боковые грани — равные прямоугольники.

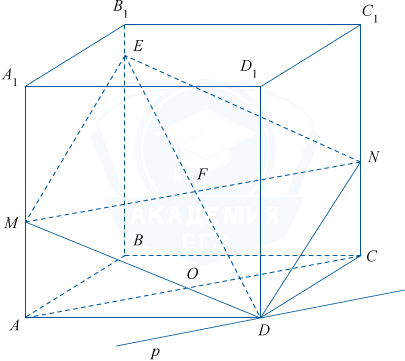
Так как плоскость сечения проходит через точки M и D параллельно диагонали AC, то для её построения в плоскости A_{1}AC через точку M проведём отрезок MN параллельный AC. Получим AC \parallel (MDN) по признаку параллельности прямой и плоскости.

Плоскость MDN пересекает параллельные плоскости A_{1}AD и B_{1}BC, тогда, по свойству параллельных плоскостей, линии пересечения граней A_{1}ADD_{1} и B_{1}BCC_{1} плоскостью MDN параллельны.

Проведём отрезок NE параллельно отрезку MD.

Четырехугольник DMEN — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC \parallel MN, следовательно, AC \parallel p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). BD \perp AC как диагонали квадрата, значит, BD \perp p. BD — проекция ED на плоскость ABC, тогда по теореме о трех перпендикулярах ED \perp p, следовательно, \angle EDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.

Установим вид четырехугольника DMEN. MD \parallel EN, аналогично ME \parallel DN, значит, DMEN — параллелограмм, а так как MD=DN (прямоугольные треугольники MAD и NCD равны по двум катетам: AD=DC как стороны квадрата, AM=CN как расстояния между параллельными прямыми AC и MN), следовательно, DMEN — ромб. Отсюда, F — середина MN.

По условию AM:MA_{1}=2:3, тогда AM=\frac{2}{5}AA_{1}=\frac{2}{5} \cdot 5\sqrt{6}=2\sqrt{6}.

AMNC — прямоугольник, F — середина MN, O — середина AC. Значит, FO\parallel MA,  FO \perp AC,  FO=MA=2\sqrt{6}.

Зная, что диагональ квадрата равна a\sqrt{2}, где a — сторона квадрата, получим BD=4\sqrt{2}. OD=\frac{1}{2}BD=\frac{1}{2} \cdot 4\sqrt{2}=2\sqrt{2}.

В прямоугольном треугольнике FOD\enspace tg \angle FDO=\frac{FO}{OD}=\frac{2\sqrt{6}}{2\sqrt{2}}=\sqrt{3}. Следовательно, \angle FDO=60^\circ.

60^\circ

а) Рассмотрим рисунок.

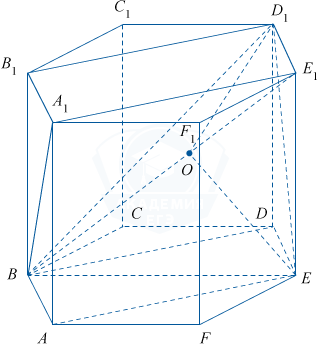
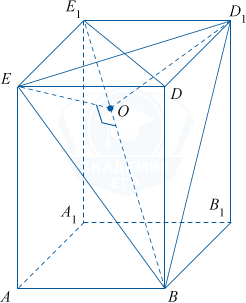
Заметим, что параллелепипед ABB_{1}A_{1}EDD_{1}E_{1} является правильной призмой (ABB_{1}A_{1} — квадрат). BD \perp EDD_{1}, тогда BD \perp ED_{1}, ED_{1} \perp ED как диагонали квадрата, значит, ED_{1} \perp A_{1}BD, следовательно, ED_{1} \perp BE_{1}, и угол между ними прямой.

б) Рассмотрим двугранный угол EE_{1}BD_{1} и его линейный угол EOD_{1}. С помощью теоремы косинусов можно найти высоту AE=\sqrt{3} параллелепипеда. Диагональ боковой грани BE=\sqrt{BA^{2}+AE^{2}}=2 и диагональ BE_{1}=\sqrt{BE^{2}+EE_{1}^{2}}=\sqrt{5} параллелепипеда.

В прямоугольном треугольнике с известными катетами BE=2, EE_{1}=1 и гипотенузой BE_{1}=\sqrt{5} найдем высоту EO=\frac{BE \cdot EE_{1}}{BE_{1}}=\frac{2}{\sqrt{5}}.

Из равенства треугольников BEE_{1} и E_{1}BD_{1} следует, что треугольник EOD_{1}является равнобедренным OE=OD_{1}=\frac{2}{\sqrt{5}} с основанием ED_{1}=\sqrt{ED^{2}+DD_{1}^{2}}=\sqrt{2}.

Применяя теорему косинусов ED_{1}^{2}= EO^{2}+OD^{2}-2EOD_{1} \cos \angle EOD_{1}, найдем \cos EOD_{1}=-\frac{1}{4}, значит, угол между плоскостями ABD_{1} и BB_{1}E равен arccos\frac{1}{4}.

 arccos\frac14

а) В плоскости грани AA_1B_1B через точку A проведем прямую, параллельную A_1B. Q и K — точки пересечения этой прямой соответственно с прямыми A_1B_1 и BB_1.

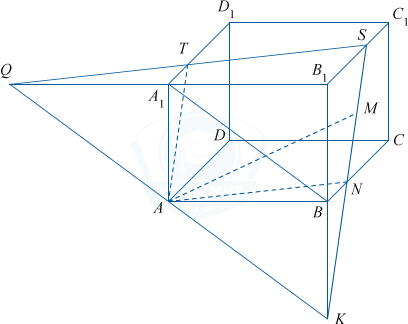
Прямая KM пересекает ребро BC в точке N, а ребро B_1C_1 — в точке S. Отрезок SQ пересекает ребро A_1D_1 в точке T.

Четырехугольник ATSN образует искомое сечение, так как все его вершины лежат в плоскости QSK, которая проходит через AM и прямую AK, параллельную A_1B, и, следовательно (QSK)\parallel A_1B.

б) 1) В плоскости грани AA_1B_1B построим отрезок AK \parallel A_1B. A_1B\parallel (AMK), AK=A_1B.

2) В плоскости BCC_1 проведем BR\perp MK, тогда по теореме, обратной теореме о трех перпендикулярах, AR \perp MK как наклонная к плоскости BCC_1, проекция которой BR\perp MK по построению.

3) Плоскость ABR \perp MK, следовательно, любая прямая плоскости ABR перпендикулярна прямой MK.

4) Проведем отрезок BH\perp AR. Длина этого отрезка — искомое расстояние.

Действительно, отрезок BH перпендикулярен двум пересекающимся прямым (AR и MK) плоскости AMK, параллельной A_1B.

5) Из \bigtriangleup MBK найдем высоту BR:

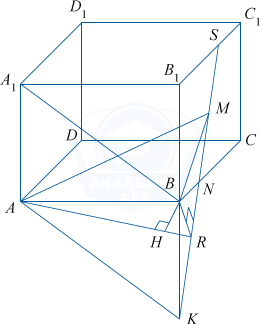
MB=2\sqrt{2}, BK=4, \angle MBK = 135^{\circ}. По теореме косинусов MK= \sqrt{MB^2+KB^2-2MB\cdot KB\cdot \cos 135^{\circ}}= \sqrt{8+16-2\cdot 2\sqrt{2}\cdot 4\cdot \left(-\frac{\sqrt{2}}{2}\right)}= 2\sqrt{10}.

S_{MBK}= \frac{1}{2}MB\cdot BK\cdot \sin 135^{\circ}= \frac{1}{2}\cdot 2\sqrt{2}\cdot 4\cdot \frac{\sqrt{2}}{2}= 4,

S_{MBK}= \frac{1}{2}MK\cdot BR= \frac{1}{2}\cdot 2\sqrt{10}\cdot BR = BR\cdot \sqrt{10}.

\sqrt{10}\cdot BR=4, откуда BR=\frac{2\sqrt{10}}{5}.

Из прямоугольного \bigtriangleup ABR высоту BH найдем из условия AB\cdot BR=AR\cdot BH.

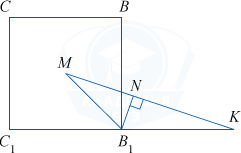
По теореме Пифагора из \bigtriangleup ABR\; AR=\sqrt{AB^2+BR^2}=\sqrt{\frac{88}{5}}, тогда 4\cdot \frac{2\sqrt{10}}{5}=\sqrt{\frac{88}{5}}\cdot BH, BH=\frac{4\sqrt{11}}{11}.

\frac{4\sqrt{11}}{11}

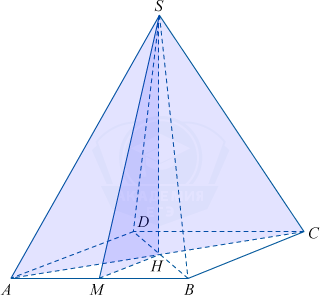
Найдем площадь основания пирамиды 144 − 108 = 36, исходя из этого AB = 6.

Определим площадь боковой грани \frac{108}{4}=27.

Примем SM за высоту SAB. Получим S_{SAB}=\frac{SM\cdot AB}{2}=SM\cdot 3=27, поэтому SM = 9.

а) Пусть SH – высота пирамиды, H – середина основания. Исходя из этого SH – прямая, по которой пересекаются данные плоскости, так же она перпендикулярна прямым AH и MH и другим прямым, лежащим в плоскости основания пирамиды. От сюда следует, что угол между плоскостью SAC и плоскостью SMH – это угол AHM, который равен 45^{\circ}.

б) SH=\sqrt{SM^{2}-MH^{2}}=\sqrt{72}=6\sqrt{2}.

Получаем S_{SAC}=\frac{SH\cdot AC}{2}=6\sqrt{2}\cdot 3\sqrt{2}=36.

а) 45^{\circ}; б) 36