Задание №234

а) Рассмотрим рисунок.

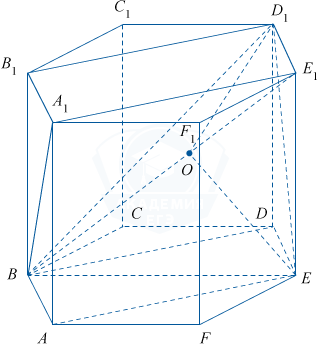
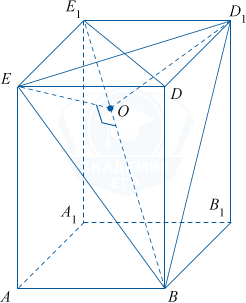
Заметим, что параллелепипед ABB_{1}A_{1}EDD_{1}E_{1} является правильной призмой (ABB_{1}A_{1} — квадрат). BD \perp EDD_{1}, тогда BD \perp ED_{1}, ED_{1} \perp ED как диагонали квадрата, значит, ED_{1} \perp A_{1}BD, следовательно, ED_{1} \perp BE_{1}, и угол между ними прямой.

б) Рассмотрим двугранный угол EE_{1}BD_{1} и его линейный угол EOD_{1}. С помощью теоремы косинусов можно найти высоту AE=\sqrt{3} параллелепипеда. Диагональ боковой грани BE=\sqrt{BA^{2}+AE^{2}}=2 и диагональ BE_{1}=\sqrt{BE^{2}+EE_{1}^{2}}=\sqrt{5} параллелепипеда.

В прямоугольном треугольнике с известными катетами BE=2, EE_{1}=1 и гипотенузой BE_{1}=\sqrt{5} найдем высоту EO=\frac{BE \cdot EE_{1}}{BE_{1}}=\frac{2}{\sqrt{5}}.

Из равенства треугольников BEE_{1} и E_{1}BD_{1} следует, что треугольник EOD_{1}является равнобедренным OE=OD_{1}=\frac{2}{\sqrt{5}} с основанием ED_{1}=\sqrt{ED^{2}+DD_{1}^{2}}=\sqrt{2}.

Применяя теорему косинусов ED_{1}^{2}= EO^{2}+OD^{2}-2EOD_{1} \cos \angle EOD_{1}, найдем \cos EOD_{1}=-\frac{1}{4}, значит, угол между плоскостями ABD_{1} и BB_{1}E равен arccos\frac{1}{4}.

 arccos\frac14