Задание №199

а) В плоскости грани AA_1B_1B через точку A проведем прямую, параллельную A_1B. Q и K — точки пересечения этой прямой соответственно с прямыми A_1B_1 и BB_1.

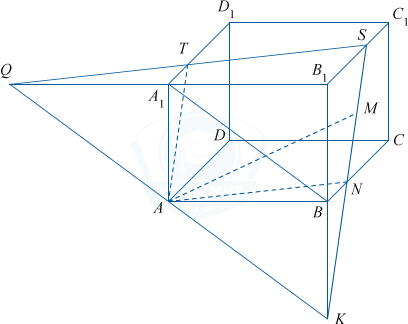
Прямая KM пересекает ребро BC в точке N, а ребро B_1C_1 — в точке S. Отрезок SQ пересекает ребро A_1D_1 в точке T.

Четырехугольник ATSN образует искомое сечение, так как все его вершины лежат в плоскости QSK, которая проходит через AM и прямую AK, параллельную A_1B, и, следовательно (QSK)\parallel A_1B.

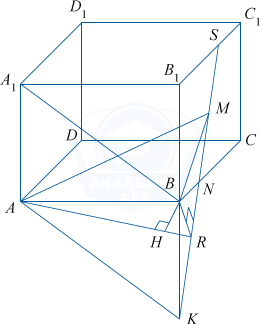
б) 1) В плоскости грани AA_1B_1B построим отрезок AK \parallel A_1B. A_1B\parallel (AMK), AK=A_1B.

2) В плоскости BCC_1 проведем BR\perp MK, тогда по теореме, обратной теореме о трех перпендикулярах, AR \perp MK как наклонная к плоскости BCC_1, проекция которой BR\perp MK по построению.

3) Плоскость ABR \perp MK, следовательно, любая прямая плоскости ABR перпендикулярна прямой MK.

4) Проведем отрезок BH\perp AR. Длина этого отрезка — искомое расстояние.

Действительно, отрезок BH перпендикулярен двум пересекающимся прямым (AR и MK) плоскости AMK, параллельной A_1B.

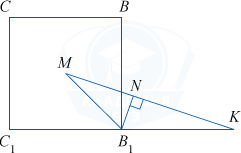
5) Из \bigtriangleup MBK найдем высоту BR:

MB=2\sqrt{2}, BK=4, \angle MBK = 135^{\circ}. По теореме косинусов MK= \sqrt{MB^2+KB^2-2MB\cdot KB\cdot \cos 135^{\circ}}= \sqrt{8+16-2\cdot 2\sqrt{2}\cdot 4\cdot \left(-\frac{\sqrt{2}}{2}\right)}= 2\sqrt{10}.

S_{MBK}= \frac{1}{2}MB\cdot BK\cdot \sin 135^{\circ}= \frac{1}{2}\cdot 2\sqrt{2}\cdot 4\cdot \frac{\sqrt{2}}{2}= 4,

S_{MBK}= \frac{1}{2}MK\cdot BR= \frac{1}{2}\cdot 2\sqrt{10}\cdot BR = BR\cdot \sqrt{10}.

\sqrt{10}\cdot BR=4, откуда BR=\frac{2\sqrt{10}}{5}.

Из прямоугольного \bigtriangleup ABR высоту BH найдем из условия AB\cdot BR=AR\cdot BH.

По теореме Пифагора из \bigtriangleup ABR\; AR=\sqrt{AB^2+BR^2}=\sqrt{\frac{88}{5}}, тогда 4\cdot \frac{2\sqrt{10}}{5}=\sqrt{\frac{88}{5}}\cdot BH, BH=\frac{4\sqrt{11}}{11}.

\frac{4\sqrt{11}}{11}