Задание №159
Условие
Площадь полной поверхности правильной четырехугольной пирамиды SABCD с основанием ABCD равна 144, а площадь боковой поверхности равна 108.
а) Докажите, что угол между плоскостью SAC и плоскостью, которая проходит через вершину S данной пирамиды, середину стороны AB и центр основания, равен 45^{\circ}.
б) Найдите чему равна площадь сечения пирамиды плоскостью SAC.
Решение
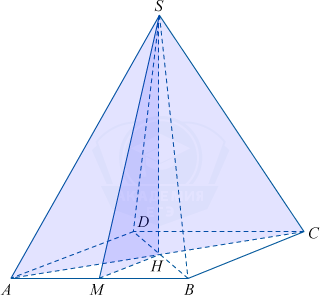
Найдем площадь основания пирамиды 144 − 108 = 36, исходя из этого AB = 6.
Определим площадь боковой грани \frac{108}{4}=27.
Примем SM за высоту SAB. Получим S_{SAB}=\frac{SM\cdot AB}{2}=SM\cdot 3=27, поэтому SM = 9.
а) Пусть SH – высота пирамиды, H – середина основания. Исходя из этого SH – прямая, по которой пересекаются данные плоскости, так же она перпендикулярна прямым AH и MH и другим прямым, лежащим в плоскости основания пирамиды. От сюда следует, что угол между плоскостью SAC и плоскостью SMH – это угол AHM, который равен 45^{\circ}.
б) SH=\sqrt{SM^{2}-MH^{2}}=\sqrt{72}=6\sqrt{2}.
Получаем S_{SAC}=\frac{SH\cdot AC}{2}=6\sqrt{2}\cdot 3\sqrt{2}=36.
Ответ
а) 45^{\circ}; б) 36
Инесса Степанова /
Инесса Степанова /