Задание №981

а) По условию ABCDA_{1}B_{1}C_{1}D_{1} — правильная призма, это означает, что основание ABCD — квадрат и боковые грани — равные прямоугольники.

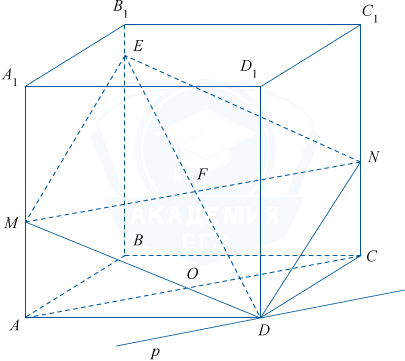
Так как плоскость сечения проходит через точки M и D параллельно диагонали AC, то для её построения в плоскости A_{1}AC через точку M проведём отрезок MN параллельный AC. Получим AC \parallel (MDN) по признаку параллельности прямой и плоскости.

Плоскость MDN пересекает параллельные плоскости A_{1}AD и B_{1}BC, тогда, по свойству параллельных плоскостей, линии пересечения граней A_{1}ADD_{1} и B_{1}BCC_{1} плоскостью MDN параллельны.

Проведём отрезок NE параллельно отрезку MD.

Четырехугольник DMEN — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC \parallel MN, следовательно, AC \parallel p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). BD \perp AC как диагонали квадрата, значит, BD \perp p. BD — проекция ED на плоскость ABC, тогда по теореме о трех перпендикулярах ED \perp p, следовательно, \angle EDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.

Установим вид четырехугольника DMEN. MD \parallel EN, аналогично ME \parallel DN, значит, DMEN — параллелограмм, а так как MD=DN (прямоугольные треугольники MAD и NCD равны по двум катетам: AD=DC как стороны квадрата, AM=CN как расстояния между параллельными прямыми AC и MN), следовательно, DMEN — ромб. Отсюда, F — середина MN.

По условию AM:MA_{1}=2:3, тогда AM=\frac{2}{5}AA_{1}=\frac{2}{5} \cdot 5\sqrt{6}=2\sqrt{6}.

AMNC — прямоугольник, F — середина MN, O — середина AC. Значит, FO\parallel MA,  FO \perp AC,  FO=MA=2\sqrt{6}.

Зная, что диагональ квадрата равна a\sqrt{2}, где a — сторона квадрата, получим BD=4\sqrt{2}. OD=\frac{1}{2}BD=\frac{1}{2} \cdot 4\sqrt{2}=2\sqrt{2}.

В прямоугольном треугольнике FOD\enspace tg \angle FDO=\frac{FO}{OD}=\frac{2\sqrt{6}}{2\sqrt{2}}=\sqrt{3}. Следовательно, \angle FDO=60^\circ.

60^\circ