Задание №983
Условие
Основанием прямой призмы ABCDA_{1}B_{1}C_{1}D_{1} является ромб с тупым углом B, равным 120^\circ. Все ребра этой призмы равны 10. Точки P и K — середины ребер CC_{1} и CD соответственно.
а) Докажите, что прямые PK и PB_{1} перпендикулярны.
б) Найдите угол между плоскостями PKB_{1} и C_{1}B_{1}B.
Решение
а) Будем использовать метод координат. Найдём скалярное произведение векторов \vec{PK} и \vec{PB_{1}}, а затем косинус угла между этими векторами. Направим ось Oy вдоль CD, ось Oz вдоль CC_{1}, и ось Ox \perp CD. C — начало координат.
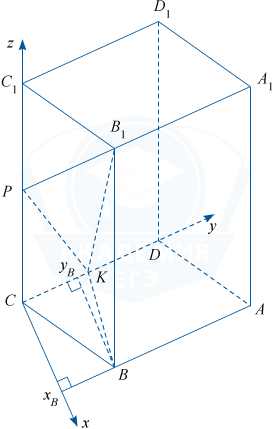
Тогда C (0;0;0); C_{1}(0;0;10); P(0;0;5); K(0;5;0); B(BC \cos 30^\circ; BC\sin 30^\circ; 0), то есть B(5\sqrt{3}; 5;0), B_{1}(5\sqrt{3}; 5;10).
Найдём координаты векторов: \vec{PK}=\{0;5;-5\}; \vec{PB_{1}}=\{5\sqrt{3}; 5;5\}.
Пусть угол между \vec{PK} и \vec{PB_{1}} равен \alpha.
Получаем \cos \alpha=\frac{\vec{PK} \cdot \vec{PB_{1}}}{|\vec{PK}| \cdot |\vec{PB_{1}}|}= \frac{0 \cdot 5\sqrt{3} + 5 \cdot 5-5 \cdot 5}{|\vec{PK}| \cdot |\vec{PB_{1}}|}=0.
\cos \alpha =0, значит, \vec{PK} \perp \vec{PB_{1}} и прямые PK и PB_{1} перпендикулярны.
б) Угол между плоскостями равен углу между ненулевыми векторами, перпендикулярными этим плоскостям (или, если угол тупой, смежному с ним углу). Такие векторы называют нормалями к плоскостям. Найдём их.
Пусть \vec{n_{1}}=\{x; y; z\} перпендикулярен плоскости PKB_{1}. Найдем его, решив систему \begin{cases} \vec{n_{1}} \perp \vec{PK}, \\ \vec{n_{1}} \perp \vec{PB_{1}}. \end{cases}
\begin{cases} \vec{n_{1}} \cdot \vec{PK}=0, \\ \vec{n_{1}} \cdot \vec{PB_{1}}=0; \end{cases}
\begin{cases} 0x+5y-5z=0, \\ 5\sqrt{3}x+5y+5z=0; \end{cases}
\begin{cases}y=z, \\ x=\frac{-y-z}{\sqrt{3}}. \end{cases}
Возьмем y=1; z=1; x=\frac{-2}{\sqrt{3}}, \vec{n_{1}}=\left \{ \frac{-2}{\sqrt{3}}; 1;1 \right \}.
Пусть \vec{n_{2}}=\{x; y; z\} перпендикулярен плоскости C_{1}B_{1}B. Найдем его, решив систему \begin{cases} \vec{n_{2}} \perp \vec{CC_{1}}, \\ \vec{n_{2}} \perp \vec{CB}. \end{cases}
\vec{CC_{1}}=\{0;0;10\}, \vec{CB}=\{5\sqrt{3}; 5; 0\}.
\begin{cases} \vec{n_{2}} \cdot \vec{CC_{1}}=0, \\ \vec{n_{2}} \cdot \vec{CB}=0; \end{cases}
\begin{cases} 0x+0y+10z=0, \\ 5\sqrt{3}x+5y+0z=0; \end{cases}
\begin{cases}z=0, \\ y=-\sqrt{3}x. \end{cases}
Возьмем x=1; y=-\sqrt{3}; z=0, \vec{n_{2}}=\{1; -\sqrt{3};0\}.
Найдем косинус искомого угла \beta (он равен модулю косинуса угла между \vec{n_{1}} и \vec{n_{2}}).
\cos \beta= \frac{|\vec{n_{1}} \cdot \vec{n_{2}}|}{|\vec{n_{1}}| \cdot |\vec{n_{2}}|}= \frac{\left |-\dfrac{2}{\sqrt{3}}\cdot 1+1 \cdot (-\sqrt{3})+1 \cdot 0 \right |}{\sqrt{\dfrac{4}{3}+1+1} \cdot \sqrt{1+3+0}}= \frac{\dfrac{5}{\sqrt{3}}}{2\sqrt{\dfrac{10}{3}}}= \frac{\sqrt{10}}{4}.
\cos \beta =\frac{\sqrt{10}}{4}, \beta=\arccos\frac{\sqrt{10}}{4}.
Ответ
\arccos\frac{\sqrt{10}}{4}