Задание №986

а) Пусть D и E — середины ребер AC и BB_{1} соответственно.

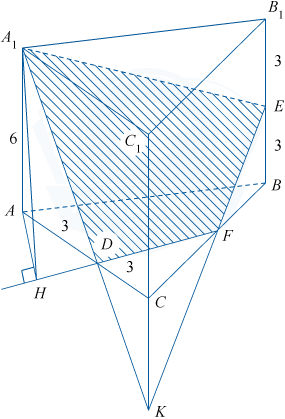
В плоскости AA_{1}C_{1} проведем прямую A_{1}D, которая пересекает прямую CC_{1} в точке K, в плоскости BB_{1}C_{1} — прямую KE, которая пересекает ребро BC в точке F. Соединие точки A_{1} и E, лежащие в плоскости AA_{1}B_{1}, а также D и F, лежащие в плоскости ABC, получим сечение A_{1}EFD.

\bigtriangleup AA_{1}D=\bigtriangleup CDK по катету AD=DC и острому углу.

\angle ADA_{1}=\angle CDK — как вертиальные, отсюда следует, что AA_{1}=CK=6. \bigtriangleup CKF и \bigtriangleup BFE подобны по двум углам \angle FBE=\angle KCF=90^\circ, \angle BFE=\angle CFK — как вертикальные.

\frac{CK}{BE}=\frac{6}{3}=2, то есть коэффициент подобия равен 2, откуда следует, что CF:FB=2:1.

б) Проведём AH \perp DF. Угол между плоскостью сечения и плоскостью основания равен углу AHA_{1}. Действительно, отрезок AH \perp DF (DF — линия пересечения этих плоскостей) и является проекцией отрезка A_{1}H на плоскость основания, следовательно, по теореме о трёх перпендикулярах, A_{1}H \perp DF. \angle AHA_{1}=arctg\frac{AA_{1}}{AH}. AA_{1}=6.

Найдём AH. \angle ADH =\angle FDC (как вертикальные).

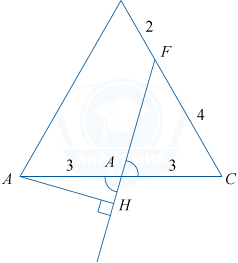
По теореме косинусов в \bigtriangleup DFC:

DF^2=FC^2+DC^2- 2FC \cdot DC \cdot \cos 60^\circ,

DF^2=4^2+3^2-2 \cdot 4 \cdot 3 \cdot \frac{1}{2}=13.

FC^2=DF^2+DC^2- 2DF \cdot DC \cdot \cos \angle FDC,

4^2=13+9-2\sqrt{13} \cdot 3 \cdot \cos \angle FDC,

\cos \angle FDC=\frac{6}{2\sqrt{13} \cdot 3}=\frac{1}{\sqrt{13}}.

По следствию из основного тригонометрического тождества

\sin \angle FDC=\sqrt{1-\left ( \frac{1}{\sqrt{13}}\right )^2}=\frac{2\sqrt{3}}{\sqrt{13}}. Из \bigtriangleup ADH найдём AH:

AH=AD \cdot \sin \angle ADH, (\angle FDC=\angle ADH). AH=3 \cdot \frac{2\sqrt{3}}{\sqrt{13}}=\frac{6\sqrt{13}}{\sqrt{13}}.

\angle AHA_{1}= arctg\frac{AA_{1}}{AH}= arctg\frac{6 \cdot \sqrt{13}}{6\sqrt{3}}= arctg\frac{\sqrt{39}}{3}.

arctg\frac{\sqrt{39}}{3}.