Задание №1183
Условие
Дана правильная четырёхугольная пирамида KMNPQ со стороной основания MNPQ, равной 6, и боковым ребром 3\sqrt {26}.
а) Постройте сечение пирамиды плоскостью, проходящей через прямую NF параллельно диагонали MP, если точка F — середина ребра MK.
б) Найдите величину угла между плоскостью сечения и плоскостью KMP.
Решение
а) Пусть KO — высота пирамиды, F — середина MK; FE \parallel MP (в плоскости PKM ). Так как FE — средняя линия \triangle PKM, то FE=\frac{MP}2.
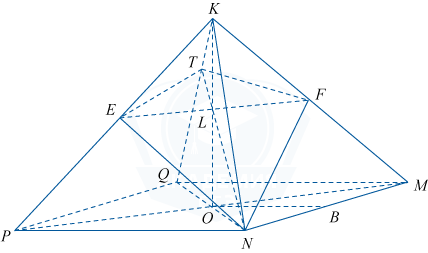
Построим сечение пирамиды плоскостью, проходящей через NF и параллельной MP, то есть плоскостью NFE. L — точка пересечения EF и KO. Так как точки L и N принадлежат искомому сечению и лежат в плоскости KQN, то точка T, полученная как пересечение LN и KQ, является также точкой пересечения искомого сечения и ребра KQ. NETF — искомое сечение.
б) Плоскости NFE и MPK пересекаются по прямой FE. Значит, угол между этими плоскостями равен линейному углу двугранного угла OFEN, построим его: LO \perp MP, MP \parallel FE, следовательно, LO \perp FE; \triangle NFE — равнобедренный (NE=NF как соответствующие медианы равных треугольников KPN и KMN ), NL — его медиана (EL=LF, так как PO=OM, а \triangle KEF \sim \triangle KPM ). Отсюда NL \perp FE и \angle NLO — искомый.
ON=\frac12QN=\frac12MN\sqrt 2=3\sqrt 2.
\triangle KON — прямоугольный.
Катет KO по теореме Пифагора равен KO=\sqrt {KN^2-ON^2}.
OL= \frac12KO= \frac12\sqrt{KN^2-ON^2}= \frac12\sqrt {9\cdot 26-9\cdot 2}= \frac12\sqrt{9(26-2)}= \frac32\sqrt {24}= \frac32\cdot 2\sqrt 6= 3\sqrt 6.
tg\angle NLO =\frac{ON}{OL}=\frac{3\sqrt 2}{3\sqrt 6}=\frac1{\sqrt 3},
\angle NLO=30^{\circ}.
Ответ
30