Задание №1188
Условие
Дана правильная призма ABCDA_1B_1C_1D_1, M и N — середины ребер AB и BC соответственно, точка K — середина MN.
а) Докажите, что прямые KD_1 и MN перпендикулярны.
б) Найдите угол между плоскостями MND_1 и ABC, если AB=8, AA_1=6\sqrt 2.
Решение
а) В \triangle DCN и \triangle MAD имеем: \angle C=\angle A=90^{\circ}, CN=AM=\frac12AB, CD=DA.
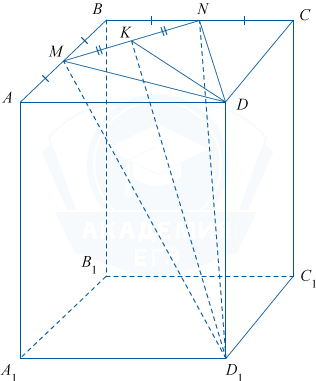
Отсюда \triangle DCN=\triangle MAD по двум катетам. Тогда MD=DN, \triangle DMN равнобедренный. Значит, медиана DK — является также высотой. Следовательно, DK \perp MN.
DD_1 \perp MND по условию, D_1K — наклонная, KD — проекция, DK \perp MN.
Отсюда по теореме о трех перпендикулярах MN\perp D_1K.
б) Как было доказано в а), DK \perp MN и MN \perp D_1K, но MN — линия пересечения плоскостей MND_1 и ABC, значит \angle DKD_1 — линейный угол двугранного угла между плоскостями MND_1 и ABC.
В \triangle DAM по теореме Пифагора DM= \sqrt {DA^2+AM^2}= \sqrt {64+16}= 4\sqrt 5, MN= \sqrt {MB^2+BN^2}= \sqrt {16+16}= 4\sqrt 2. Следовательно, в \triangle DKM по теореме Пифагора DK= \sqrt {DM^2-KM^2}= \sqrt {80-8}= 6\sqrt 2. Тогда в \triangle DKD_1, tg\angle DKD_1=\frac{DD_1}{DK}=\frac{6\sqrt 2}{6\sqrt 2}=1.
Значит, \angle DKD_1=45^{\circ}.
Ответ
45^{\circ}.