Задания по теме «Тригонометрические функции»

Найдём производную исходной функции:

y'= (12x)'-12(tg x)'-(18)'= 12-\frac{12}{\cos ^2x}= \frac{12\cos ^2x-12}{\cos ^2x}\leqslant0. Значит, исходная функция является невозрастающей на рассматриваемом промежутке и принимает наибольшее значение на левом конце отрезка, то есть при x=0. Наибольшее значение равно y(0)= 12\cdot 0-12 tg (0)-18= -18.

Найдём производную исходной функции:

y'= 32(tg x)'-(32x)'-(8\pi )'+(103)'= \frac{32}{\cos ^2x}-32= \frac{32-32\cos ^2x}{\cos ^2x}\geqslant0. Значит, исходная функция является неубывающей на рассматриваемом промежутке и принимает

наименьшее значение на левом конце отрезка, то есть при x=-\frac{\pi}{4}. Наименьшее значение равно y\left(-\frac{\pi}{4}\right)= 32tg\left(-\frac{\pi}{4}\right)-32\cdot\left(-\frac{\pi}{4}\right)-8\pi+103= -32+103= 71.

Найдём производную исходной функции: y'= (0,7-x)' \cos x\,+ (0,7-x)(\cos x)'+(\sin x)'+(2)' = -\cos x+(0,7-x)\cdot (- \sin x)+ \cos x= (x-0,7) \sin x. Найдём нули производной на интервале \left(0; \frac{\pi}{2}\right), учитывая, что на этом множестве \sin x>0.

Имеем (x-0,7) \sin x=0;

x-0,7=0;

x=0,7.

Значение x=0,7 принадлежит интервалу \left(0; \frac{\pi}{2}\right). При x \in (0; 0,7) выполняется неравенство y'(x)<0. При x \in \left(0,7; \frac{\pi}{2}\right) выполняется неравенство y'(x)>0.

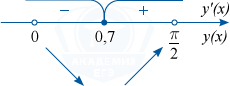
Отсюда x=0,7 является единственной точкой минимума на рассматриваемом интервале.

Найдём производную исходной функции: y'=-9+9\sqrt 2 \sin x. Вычислим нули производной: y'=0;

-9+9\sqrt 2\sin x=0;

\sin x=\frac{\sqrt2}{2}.

На отрезке \left[0; \frac{\pi}{2}\right] этому уравнению удовлетворяет только x=\frac{\pi}{4}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.

Из рисунка видно, что при x<\frac{\pi}{4} выполняется y'(x)<0 и исходная функция убывает. Аналогично, при x>\frac{\pi}{4} выполняется y'(x)>0 и исходная функция возрастает. Значит, наименьшее значение достигается при x=\frac{\pi}{4} и равно y\left(\frac{\pi}{4}\right)= 24+\frac{9\pi}{4}-9\cdot\frac{\pi}{4}-9\sqrt2\cos \frac{\pi}{4}= 24-9=15.

Найдём производную исходной функции: y'= (4x-5)'\cos x+(4x-5)(\cos x)'-4(\sin x)'+(12)'= 4\cos x+(4x-5)\cdot(-\sin x)-4\cos x= -(4x-5)\sin x.

Найдём нули производной на интервале \left ( 0; \frac{\pi}{2} \right ), учитывая, что на этом множестве \sin x>0.

Имеем -(4x-5)\sin x=0,

4x-5=0,

x=\frac54.

Значение x=\frac54 принадлежит интервалу \left ( 0; \frac{\pi}{2} \right ). При x\in\left ( 0; \frac54 \right ) выполняется неравенство y'(x)>0. При x\in\left ( \frac54; \frac{\pi}{2} \right ) выполняется неравенство y'(x)<0. Отсюда x=\frac54=1,25 является единственной точкой максимума на рассматриваемом интервале.

Найдём производную исходной функции: y'=-18\sin x+9\sqrt3. Вычислим нули производной: y'=0.

-18\sin x+9\sqrt3=0,

\sin x=\frac{\sqrt3}{2}.

На отрезке \left [ 0; \frac{\pi}{2} \right ] этому уравнению удовлетворяет только x=\frac{\pi}{3}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.

Из рисунка видно, что при x<\frac{\pi}{3} выполняется y'(x)>0 и исходная функция возрастает. Аналогично при x>\frac{\pi}{3} выполняется y'(x)<0 и исходная функция убывает. Значит, наибольшее значение достигается при x=\frac{\pi}{3} и равно y\left ( \frac{\pi}{3} \right )= 18\cos\frac{\pi}{3}+9\sqrt3\cdot\frac{\pi}{3}-3\sqrt3 \pi+16= 9+16=25.

Вычислим производную функции.

y'=\frac{13}{\cos^2x}-13=13(\frac{1}{\cos^2x}-1)=13tg^2x

Производная функции на всем промежутке возрастает, значит наибольшее значение функции она достигает на правом конце отрезка. Вычислим значение функции в этой точке.

y(0)=13tg0-13\cdot0+5=5

Точка 5 – наибольшее значение функции.

Вычислим производную функции.

y'=-8\sin x-17

Так как выражение -8\sin x при любых значениях x всегда не больше чем 8, то полученная разность меньше нуля, а это говорит о том, что функция убывает. Следовательно наименьшее значение функция достигает на правом конце отрезка. Вычислим это значение.

y(0)=8\cos0-17\cdot0+6 = 8+6=14

Точка 14 – наименьшее значение функции.

Вычислим производную функции.

y'=2\cos x-(2x-3)\sin x-2\cos x

y'=-(2x-3)\sin x

y'=(3-2x)\sin x

Найдем точки экстремума, в которых производная функции обращается в нуль.

(3-2x)\sin x=0

\left [\begin{array}{l} 3-2x=0 \\ \sin x=0 \end{array} \right .

\left [\begin{array}{l} x=1,5 \\ x=\pi n, n \in \mathbb{Z} \notin \left ( 0; \frac{\pi}{2} \right) \end{array} \right .

На числовой оси отложим граничные точки промежутка и точку экстремума и посмотрим как ведет себя функция.

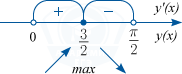
При переходе через точку x = 1,5 производная меняет знак с плюса на минус. Значит x = 1,5 – точка максимума функции.