Задание №126
Условие
Найдите точку максимума функции y=(2x-3)\cos x-2\sin x+2 на промежутке \left ( 0; \frac{\pi}{2} \right ).
Решение
Вычислим производную функции.
y'=2\cos x-(2x-3)\sin x-2\cos x
y'=-(2x-3)\sin x
y'=(3-2x)\sin x
Найдем точки экстремума, в которых производная функции обращается в нуль.
(3-2x)\sin x=0
\left [\begin{array}{l} 3-2x=0 \\ \sin x=0 \end{array} \right .
\left [\begin{array}{l} x=1,5 \\ x=\pi n, n \in \mathbb{Z} \notin \left ( 0; \frac{\pi}{2} \right) \end{array} \right .
На числовой оси отложим граничные точки промежутка и точку экстремума и посмотрим как ведет себя функция.
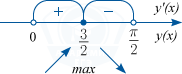
При переходе через точку x = 1,5 производная меняет знак с плюса на минус. Значит x = 1,5 – точка максимума функции.