Задание №1122

Найдём производную исходной функции: y'= (0,7-x)' \cos x\,+ (0,7-x)(\cos x)'+(\sin x)'+(2)' = -\cos x+(0,7-x)\cdot (- \sin x)+ \cos x= (x-0,7) \sin x. Найдём нули производной на интервале \left(0; \frac{\pi}{2}\right), учитывая, что на этом множестве \sin x>0.

Имеем (x-0,7) \sin x=0;

x-0,7=0;

x=0,7.

Значение x=0,7 принадлежит интервалу \left(0; \frac{\pi}{2}\right). При x \in (0; 0,7) выполняется неравенство y'(x)<0. При x \in \left(0,7; \frac{\pi}{2}\right) выполняется неравенство y'(x)>0.

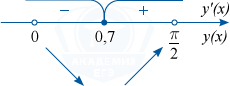
Отсюда x=0,7 является единственной точкой минимума на рассматриваемом интервале.