Задания по теме «Рациональные функции»

Исходная функция определена при x \neq 0. Тогда производная исходной функции y'(x)=1-\frac{36}{x^2}. Найдём нули производной: y'(x)=0 при \frac{36}{x^2}=1,

x^2=36,

x=\pm 6.

Исследуемому промежутку принадлежит только значение x=-6. Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=x+\frac{36}{x}+10 возрастает на промежутке [-10; -6] и убывает на промежутке [-6; -1]. Наибольшее значение достигается при x=-6 и равно y(-6)=-6+\frac{36}{-6}+10=-2.

Исходная функция определена при x \neq 0. Тогда производная исходной функции y'(x)=1-\frac{25}{x^2}. Найдём нули производной: y'(x)=0 при \frac{25}{x^2}=1,

x^2=25,

x=\pm 5.

Исследуемому промежутку принадлежит только значение x=5. Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=x+\frac{25}{x}+2017 убывает на промежутке [1; 5] и возрастает на промежутке [5; 25]. Наименьшее значение достигается при x=5 и равно y(5)=5+\frac{25}{5}+2017=2027.

Исходная функция определена при x \neq 0, при этом y=-x-\frac{10\,000}{x}. Тогда производная исходной функции y'(x)=-1+\frac{10\,000}{x^2}. Найдём нули производной: y'(x)=0 при \frac{10\,000}{x^2}=1,

x^2=10\,000,

x=\pm 100.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=-\frac{x^2+10\,000}{x} имеет единственную точку минимума x=-100.

Исходная функция определена при x\neq0, при этом y=-x-\frac{144}{x}. Тогда производная исходной функции y'(x)=-1+\frac{144}{x^2}. Найдем нули производной: y'(x)=0 при \frac{144}{x^2}=1, x^2=144, x=\pm12. Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что функция y=-\frac{x^2+144}{x} имеет единственную точку максимума x=12.

Находим производную: y'=-\frac{1\cdot(x^2+961)-x\cdot2x}{(x^2+961)^2}=\frac{x^2-961}{(x^2+961)^2}.

Решаем уравнение \frac{x^2-961}{(x^2+961)^2}=0,

x^2-961=0;

x^2=961,

x=\pm31.

Так как у дроби \frac{x^2-961}{(x^2+961)^2} знаменатель больше нуля, то ее знак совпадает со знаком числителя дроби, являющегося квадратным трехчленом x^2-961.

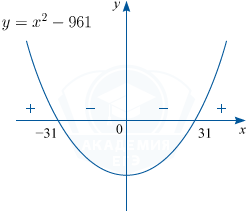
Таким образом, при y<-31 функция возрастает, а при -31<x<31 убывает, а приx>31 опять возрастает:

В точке x=-31 будет максимум.

Вычислим производную функции.

y'=-\frac{48}{x^2}+3

Найдем точки, в которых производная функции обращается в нуль.

-\frac{48}{x^2}+3=0

-\frac{48+3x^2}{x^2}=0

-48+3x^2=0

x^2=16

x=\pm4

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

При переходе через точку x = 4 производная меняет знак с минуса на плюс. Значит x = 4 – точка минимума функции.

Вычислим производную функции.

y'=-\frac{2x\cdot x-(x^2+19600)}{x^2}

y'=-\frac{x^2-19600}{x^2}

y'=-\frac{(x-140)(x+140)}{x^2}

На числовой оси отложим точки, в которых числитель и знаменатель обращается в нуль. Расставим знаки производной и посмотрим как ведет себя функция.

Производная обращается в нуль в точках −140 и 140.

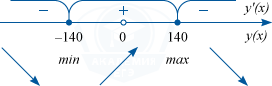
При переходе через точку x = 140 производная меняет знак с плюса на минус. Значит x = 140 – точка максимума функции.

Выполним преобразования и вычислим производную.

y=x+\frac{400}{x}

y'=1-\frac{400}{x^2}

Найдем точки, в которых производная функции обращается в нуль.

\frac{400}{x^2}=1

x^2=400

x_1=20,\enspace x_2=-20

На отрезке [-28; -2] лежит только одна точка -20.

Для нахождения наибольшего значения функции вычислим ее в граничных точках отрезка и в точке экстремума. Получим:

y(-28)= \frac{-28^2+400}{-28}= -28-\frac{400}{28}= -28-14\frac{8}{28}= -42\frac{8}{28};

y(-20)=\frac{800}{-20}=-40;

y(-2)=\frac{404}{-2}=-202;

Наибольшее значение функции равно -40.