Задание №115

Вычислим производную функции.

y'=-\frac{2x\cdot x-(x^2+19600)}{x^2}

y'=-\frac{x^2-19600}{x^2}

y'=-\frac{(x-140)(x+140)}{x^2}

На числовой оси отложим точки, в которых числитель и знаменатель обращается в нуль. Расставим знаки производной и посмотрим как ведет себя функция.

Производная обращается в нуль в точках −140 и 140.

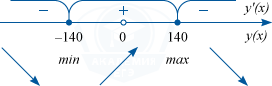
При переходе через точку x = 140 производная меняет знак с плюса на минус. Значит x = 140 – точка максимума функции.