Задание №337
Условие
Найдите точку максимума функции y=-\frac{x}{x^2+961}.
Решение
Находим производную: y'=-\frac{1\cdot(x^2+961)-x\cdot2x}{(x^2+961)^2}=\frac{x^2-961}{(x^2+961)^2}.
Решаем уравнение \frac{x^2-961}{(x^2+961)^2}=0,
x^2-961=0;
x^2=961,
x=\pm31.
Так как у дроби \frac{x^2-961}{(x^2+961)^2} знаменатель больше нуля, то ее знак совпадает со знаком числителя дроби, являющегося квадратным трехчленом x^2-961.
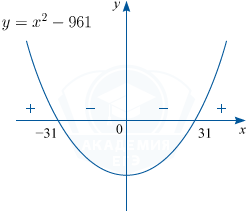
Таким образом, при y<-31 функция возрастает, а при -31<x<31 убывает, а приx>31 опять возрастает:
.png)
В точке x=-31 будет максимум.
Ответ
-31
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.