Задания по теме «Площадь сечения»

а) Так как AK=AM=5-2=3, то \triangle AKM равнобедренный.

Так как в этом равнобедренном треугольнике \angle KAM=60^{\circ}, то он равносторонний, то есть

KM=3. Тогда KM \parallel DC, так как равны соответственные углы при прямых KM, DC и секущей AD.

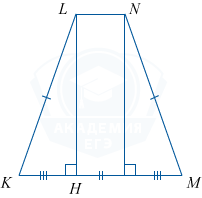
Построим LN \parallel DC. Так как в этом случае LN \parallel KM, то точки K, L, N и M лежат в одной плоскости, то есть трапеция KLNM есть искомое сечение.

б) 1. \triangle BLN \sim \triangle BDC, так как LN \parallel DC. Следовательно, \triangle BLN является равносторонним и LN=BN=BL =BD-LD=5-4=1.

2. \triangle DKL=\triangle CMN, так как DK=CM =2, DL=CN=4 и \angle KDL=\angle MCN=60^{\circ}. Значит, KL=MN и KMNL — равнобедренная трапеция.

Опустим в ней высоту LH. Отсюда, KH =\frac{KM-LN}2=\frac{3-1}2=1.

3. По теореме косинусов для \triangle KDL получим:

KL^2= KD^2+DL^2-2\cdot KD\cdot DL\cdot \cos 60^{\circ}= 2^2+4^2-2\cdot 2\cdot 4\cdot \frac12= 12.

4. По теореме Пифагора LH= \sqrt {KL^2-KH^2}= \sqrt {12-1}= \sqrt {11}.

5. S_{KMNL}= \frac12(KM+LN)\cdot LH= \frac12(3+1)\cdot \sqrt {11}= 2\sqrt {11}.

2\sqrt {11}.

а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL \parallel AC. Следовательно, искомым сечением будет трапеция AKLC.

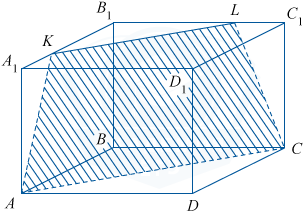
KB_1\parallel AB, B_1L\parallel BC, KL\parallel AC. Значит, треугольники KB_1L и ABC подобны и являются равнобедренными прямоугольными треугольниками. Тогда KB_1=B_1L и A_1K=C_1L. Треугольники AA_1K и CC_1L равны, следовательно, AK=CL и трапеция AKLC — равнобедренная.

б) Найдём площадь трапеции AKLC.

A_1K=\frac29A_1B_1 =\frac29\cdot 9=2.

Из \triangle AA_1K,\, AK = \sqrt {AA_1^2+A_1K^2}= \sqrt {14^2+2^2}= 10\sqrt 2.

AC=AB\sqrt 2=9\sqrt 2; KL =\frac79AC=\frac79\cdot 9\sqrt 2=7\sqrt 2.

Так как трапеция AKLC — равнобедренная, имеем

AH =\frac{AC-KL}2=\sqrt 2.

Из \triangle AKH,\, KH= \sqrt {AK^2-AH^2}= \sqrt {200-2}= \sqrt {198}.

S_{AKLC}=\frac{AC+KL}2\cdot KH\,= 8\sqrt 2\cdot \sqrt {198}=48\sqrt {11}.

48\sqrt {11}.

а) Найдём положение точки P. Эта точка пересечения плоскости FKL и ребра AB, лежащего в плоскости ABCD.

Плоскость ABCD параллельна плоскости A_1B_1C_1D_1, в которой лежит отрезок KF. Плоскость FKL пересекает параллельные плоскости ABCD и A_1B_1C_1D_1 по параллельным прямым, отсюда KF \parallel LP. Прямоугольные треугольники KD_1F и LBP равны по катету и острому углу D_1F=LB=4 и \angle D_1FK=\angle BLP как острые с соответственно параллельными сторонами).

Чтобы доказать, что четырёхугольник FKLP — прямоугольник, найдём длины его сторон и диагонали.

KF= PL= \sqrt {KD_1^2+D_1F^2}= \sqrt {16+16}= 4\sqrt 2.

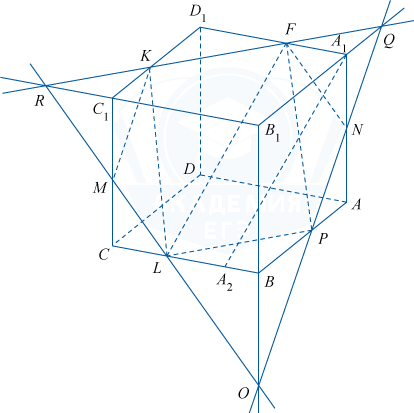
PF= LK = \sqrt {LC^2+CC_1^2+C_1K^2}= \sqrt {9+144+9}= \sqrt {162}= 9\sqrt 2. Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм. Проведём A_1A_2 \parallel LF, тогда LF= A_1A_2 = \sqrt {(LB-FA_1)^2+AB^2+AA_1^2} = \sqrt {(BP-C_1K)^2+CB^2+CC_1^2}= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.

б) Пусть Q и R — точки пересечения прямой KF и прямых B_1C_1 и A_1B_1. Проведём прямые RL и QP, они пересекут рёбра CC_1 и AA_1 в точках M и N соответственно. Тогда RC_1=KC_1=CL, поэтому можно доказать, что равны треугольники RC_1M и MCL. Прямая RL, а значит, и плоскость FKL пересекают ребро CC_1 в его середине — точке M. Аналогично плоскость FKL пересекает ребро AA_1 в его середине —точке N.

В диагональном сечении CC_1A_1A, которое является прямоугольником, отрезок MN — средняя линия. В прямоугольнике MCAN противоположные стороны равны: MN=CA=7\sqrt 2.

Сечение FKMLPN состоит из двух равных трапеций MKFN и MLPN, причём

мы доказали, что LK \perp KF и LK \perp LP. Высота каждой из этих трапеций равна \frac{LK}2=\frac{9\sqrt 2}2.

S_{\text{сечения}}= 2S_{MKFN}= 2\cdot \frac{KF+MN}2\cdot \frac{LK}2= (4\sqrt 2+7\sqrt 2)\cdot \frac{9\sqrt 2}2= 99.

99

а) Построим MN \parallel AB.

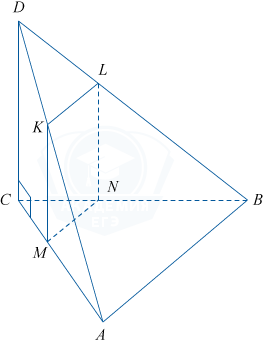
Так как KL \parallel AB по условию, то KL \parallel MN. Это означает, что точки K, L, N и M лежат в одной плоскости, то есть KLNM — искомое сечение.

б) 1. \bigtriangleup MNC \sim \bigtriangleup ABC, так как MN \parallel AB, то есть соответственные углы равны: \angle CAB=\angle CMN и \angle CBA=\angle CNM. Значит \bigtriangleup MNC равносторонний, то есть CN=MN=CM=2.

2. Аналогично можно доказать, что \bigtriangleup DKL \sim \bigtriangleup DAB, так как KL \parallel AB. Значит, \frac{KL}{AB}=\frac{DK}{DA}=\frac{2}{5}, KL=\frac{2}{5}AB=\frac{2}{5} \cdot 5=2.

3. Так как KL \parallel MN и KL=MN, то KLNM — параллелограмм.

4. \bigtriangleup AMK \sim \bigtriangleup ACD, так как угол при вершине A общий и \frac{AK}{AD}=\frac{AM}{AC}=\frac{3}{5}. Следовательно, MK \parallel CD, так как соответственные углы равны (например, \angle AKM=\angle ADC). Отсюда, MK \perp ABC, так как CD \perp ABC. Значит, MK \perp MN, то есть параллелограмм KLNM является прямоугольником.

5. По теореме Пифагора CD= \sqrt{AD^2-AC^2}= \sqrt{10^2-5^2}= 5\sqrt{3}. Так как \frac{MK}{CD}=\frac{AM}{AC}=\frac{3}{5}, то MK=\frac{3}{5}CD=3\sqrt{3}.

6. S_{KLNM}= MK \cdot MN= 3\sqrt{3} \cdot 2= 6\sqrt{3}.

6\sqrt{3}.

а) Пусть K — середина ребра SC. Так как треугольники SDC и SBC равносторонние, то SC \perp DK и SC \perp BK (медиана равностороннего треугольника является его высотой). Значит, прямая SC перпендикулярна плоскости DKB. Так как SC \perp DKB и SC \subset CSD, то плоскость DBK перпендикулярна плоскости CSD. Треугольник DKB — искомое сечение.

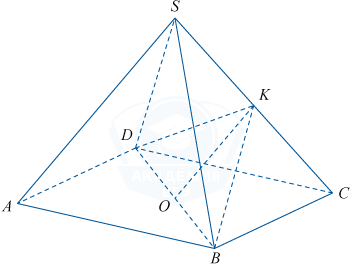
б) Найдём площадь сечения. Высоты DK и BK в равносторонних треугольниках равны \frac{5\sqrt{3}}{2}. Диагональ BD квадрата ABCD равна 5\sqrt{2}. В равнобедренном треугольнике DKB высота OK=\sqrt{\left ( \frac{5\sqrt{3}}{2}\right )^2-\left ( \frac{5\sqrt{2}}{2}\right )^2}=\frac{5}{2}. Площадь треугольника DKB равна \frac{1}{2}DB \cdot OK=\frac{1}{2} \cdot 5\sqrt{2} \cdot \frac{5}{2}=\frac{25\sqrt{2}}{4}.

\frac{25\sqrt{2}}{4}.

а) Обозначим через O точку пересечения диагоналей квадрата MNPQ.

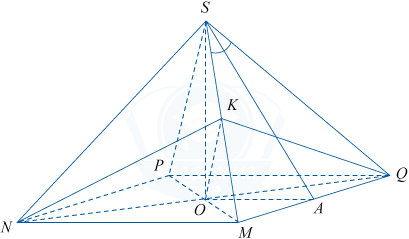
В плоскости MSP проведем через точку O прямую OK \parallel PS. Точку K соединим с точкой N и точкой Q, получим сечение NKQ, которое является искомым, так как содержит OK \parallel PS и диагональ основания NQ, по признаку параллельности прямой и плоскости: плоскость NKQ параллельна ребру PS. Данное сечение представляет собой треугольник NKQ.

б) Треугольник NKQ — равнобедренный, NK=KQ. Это следует из равенства треугольников NKM и KMQ (по двум сторонам: MK — общая, NM=MQ и углу: \angle KMQ=\angle KMN). Точка O — середина NQ, NO=OQ. KO — медиана и, следовательно, высота. S_{NKQ}=\frac{1}{2}NQ \cdot KO.

Рассмотрим \bigtriangleup SMQ, \angle MSQ=60^\circ, значит \angle SMQ=\angle SQM=60^\circ,  SM=SQ=MQ=5\sqrt{3}. \angle SOM=90^\circ, точка K — середина SM (так как OK — средняя линия \bigtriangleup PSM). Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. OK=\frac{1}{2}SM=\frac{5\sqrt{3}}{2}. NQ — диагональ квадрата со стороной 5\sqrt{3}. NQ=5\sqrt{3} \cdot \sqrt{2}=5\sqrt{6}.

S_{NKQ}= \frac{1}{2}OK \cdot NQ= \frac{5\sqrt{3} \cdot 5\sqrt{6}}{4}= \frac{75\sqrt{2}}{4}.

\frac{75\sqrt{2}}{4}

а) Построим сечение параллелепипеда плоскостью AKF.

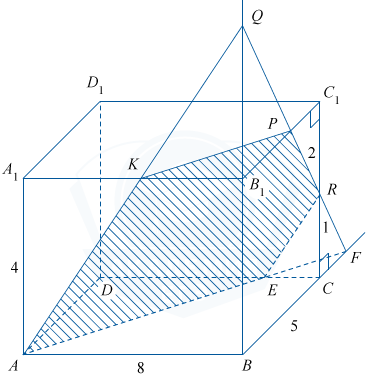
E — точка пересечения ребра DC и отрезка AF.

В плоскости ABB_1 проведем лучи AK и BB_1. AK пересекает BB_1 в точке Q. В плоскости BCC_1 проведем отрезок FQ. FQ пересекает B_1C_1 в точке P, а CC_1 в точке R. Пятиугольник AKPRE — искомое сечение.

KB_1 \parallel AB, KB_1=\frac{1}{2}A_1 B_1, значит KB_1 — средняя линия \bigtriangleup ABQ, отсюда BB_1=QB_1, а так как BF \parallel B_1 P, то B_1 P — средняя линия \bigtriangleup FBQ, BF=8, B_1 P=\frac{1}{2}BF=4. C_1 P=B_1C_1-B_1 P=5-4=1, следовательно, B_1 P:PC_1=4:1.

б) Прямоугольние треугольники ABQ, FBQ и ABF равны по двум катетам AB=BF=BQ=8, отсюда AQ=AF=QF=8\sqrt{2}.

S_{AQF}=\frac{a^{2}\sqrt{3}}{4} как площадь равностороннего треугольника со стороной a.

S_{AQF}=\frac{(8\sqrt{2})^{2} \cdot \sqrt{3}}{4}=32\sqrt{3},

S_{KQP}= \frac{1}{4}S_{AQF}= \frac{32\sqrt{3}}{4}= 8\sqrt{3}.

S_{AKPF}= S_{AQF}-S_{KQP}= 32\sqrt{3}-8\sqrt{3}= 24\sqrt{3}.

\bigtriangleup RCF \sim \bigtriangleup RC_1 P по первому признаку подобия (\angle C=\angle C_1=90^{\circ}, \angle1=\angle2 как вертикальные). Из подобия следует \frac{CF}{PC_{1}}=\frac{FR}{PR}. По доказанному в а) PC_1=1, BF=AB=8, тогда CF=8-5=3 и \frac{FR}{PR}=\frac{3}{1}. Так как KP — средняя линия \bigtriangleup AQF, то PF=\frac{1}{2}QF=4\sqrt{2}, FR=\frac{3PF}{4}=\frac{4\sqrt{2} \cdot 3}{4}=3\sqrt{2}.

В равнобедренном прямоугольном треугольнике FCE FC=EC=3, тогда EF=3\sqrt{2}. В \bigtriangleup REFFR=EF=3\sqrt{2}, \angle RFE=60^{\circ}, отсюда \bigtriangleup REF — равносторонний.S_{REF}=\frac{(3\sqrt{2})^2\sqrt{3}}{4}=\frac{9\sqrt{3}}{2}.

S_{AKPRE}= S_{AKPF}-S_{REF}= 24\sqrt{3}-\frac{9\sqrt{3}}{2}= \frac{39\sqrt{3}}{2}.

\frac{39\sqrt{3}}{2}

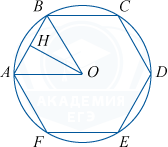
а) Пусть радиус основания равен r, O — центр основания.

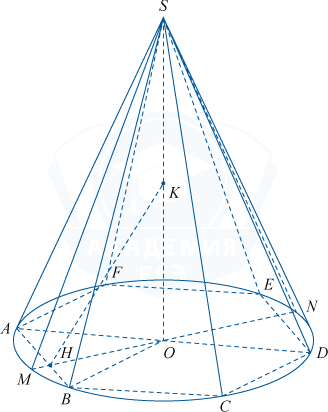
Рассмотрим правильный шестиугольник ABCDEF, OB=r, \angle BOA=60^{\circ}, \bigtriangleup AOB - равносторонний, его высота OH=\frac{OB\sqrt{3}}{2}=\frac{r\sqrt{3}}{2}. Через прямую OH и высоту конуса OS проведем осевое сечение конуса, в сечении получим \bigtriangleup SMN.

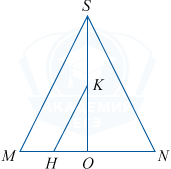
Пусть K — середина OS. \bigtriangleup SMN - равносторонний (так как образующая конуса равна диаметру его основания) со стороной 2r. Тогда SO=\frac{2r\sqrt{3}}{2}=r\sqrt{3}, OK=\frac{r\sqrt{3}}{2}, OK=OH, следовательно, прямоугольный \bigtriangleup OHK - равнобедренный \angle KHO=45^{\circ}. Так как OH — проекция KH на плоскость основания конуса, OH\perp AB по построению, то KH\perp AB по теореме о трех перпендикулярах, следовательно, \angle KHO - линейный угол двугранного угла между плоскостью \alpha и плоскостью основания конуса. Значит, двугранный угол равен 45^{\circ}, что и требовалось доказать.

б) Рассмотрим шар, вписанный в конус и осевое сечение, описанное выше. В сечении шара плоскостью MSN получим окружность, центр которой в точке Q (точке пересечения медиан \bigtriangleup MSN), OQ:QS=\frac{1}{2}, OS=r\sqrt{3}=2\sqrt{3}, SQ=\frac{4}{3}\sqrt{3}. SK=\frac{1}{2}OS=\sqrt{3}, QK=SQ-SK=\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}.

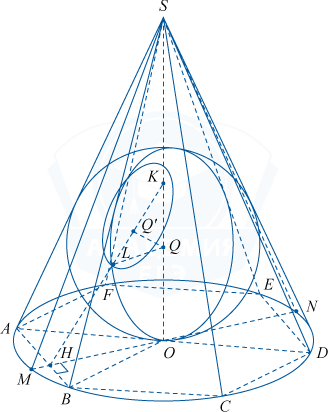
OQ=\frac{1}{3}SO=\frac{2\sqrt{3}}{3}=QL - радиус вписанного шара. Пусть QQ' \perp HK, тогда \bigtriangleup KQQ' — прямоугольный и равнобедренный (\angle QKQ'=45^{\circ}), QQ'=\frac{KQ}{\sqrt2}=\frac{1}{\sqrt{6}}, Q'L^2=QL^2-(QQ')^2=\frac{7}{6}

Q'L — радиус круга, полученного в сечении шара плоскостью \alpha. Тогда площадь сечения равна \pi Q'L^2=\frac76\pi.

б) \frac{7}{6}\pi.

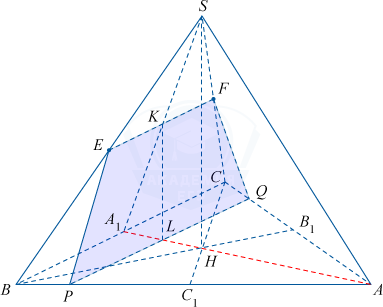
а) EF\parallel BC (как средняя линия \bigtriangleup SBC) \Rightarrow EF\parallel ABC.

Сечение пересекает плоскость основания ABC в некоторой прямой PQ \parallel EF.

Рассмотрим плоскость AA_1S.

Точка K - центр пересечения EF и A_1S, H — центр основания ABC, L – точка пересечения плоскости SAA_1 и прямой PQ.

\begin{cases} PEF \perp ABC \\ SAA_1 \perp ABC \end{cases} \Rightarrow KL \perp ABC, KL \parallel SH

FE — средняя линия \bigtriangleup SBC, A_1K=KS, следовательно, A_1L=LH (т.к. A_1H – проекция прямой A_1S на плоскость основания).

Медиана AA_1 делится точкой H в соотношении: AH:HA_1=2:1\Rightarrow AL:LA_1=5:1, ч.т.д.

б) Рассмотрим трапецию PEFQ.

EF = \frac{1}{2} BC = 12:2 = 6

\frac{PQ}{BC}=\frac{AL}{AA_1}=\frac{5}{6}

PQ=\frac{5BC}{6}=\frac{5\cdot 12}{6}=10

AH=\frac{2}{3} AA_1= \frac{2}{3}\sqrt{AB^2-(\frac{1}{2}AB)^2}= \frac{2}{3}\cdot \frac{\sqrt{3}}{2}AB= \frac{\sqrt{3}\cdot 12}{3}=4\sqrt{3}

KL=\frac{1}{2}SH= \frac{1}{2}\sqrt{SA^2-AH^2}= \frac{1}{2}\sqrt{8^2-(4\sqrt{3})^2}=2

S_{PEFQ}=\frac{1}{2}(EF+PQ)\cdot KL= \frac{1}{2}(6+10)\cdot 2=16

16