Задание №179

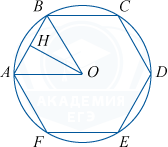
а) Пусть радиус основания равен r, O — центр основания.

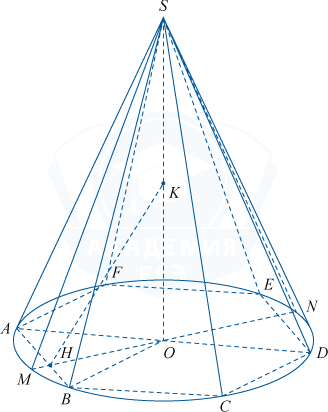
Рассмотрим правильный шестиугольник ABCDEF, OB=r, \angle BOA=60^{\circ}, \bigtriangleup AOB - равносторонний, его высота OH=\frac{OB\sqrt{3}}{2}=\frac{r\sqrt{3}}{2}. Через прямую OH и высоту конуса OS проведем осевое сечение конуса, в сечении получим \bigtriangleup SMN.

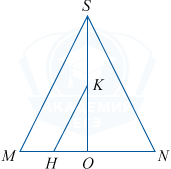
Пусть K — середина OS. \bigtriangleup SMN - равносторонний (так как образующая конуса равна диаметру его основания) со стороной 2r. Тогда SO=\frac{2r\sqrt{3}}{2}=r\sqrt{3}, OK=\frac{r\sqrt{3}}{2}, OK=OH, следовательно, прямоугольный \bigtriangleup OHK - равнобедренный \angle KHO=45^{\circ}. Так как OH — проекция KH на плоскость основания конуса, OH\perp AB по построению, то KH\perp AB по теореме о трех перпендикулярах, следовательно, \angle KHO - линейный угол двугранного угла между плоскостью \alpha и плоскостью основания конуса. Значит, двугранный угол равен 45^{\circ}, что и требовалось доказать.

б) Рассмотрим шар, вписанный в конус и осевое сечение, описанное выше. В сечении шара плоскостью MSN получим окружность, центр которой в точке Q (точке пересечения медиан \bigtriangleup MSN), OQ:QS=\frac{1}{2}, OS=r\sqrt{3}=2\sqrt{3}, SQ=\frac{4}{3}\sqrt{3}. SK=\frac{1}{2}OS=\sqrt{3}, QK=SQ-SK=\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}.

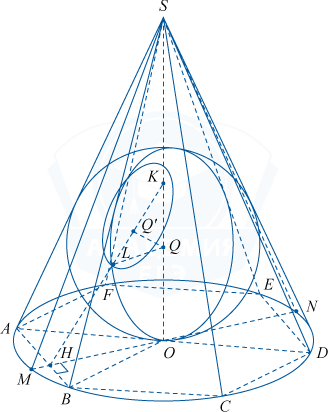
OQ=\frac{1}{3}SO=\frac{2\sqrt{3}}{3}=QL - радиус вписанного шара. Пусть QQ' \perp HK, тогда \bigtriangleup KQQ' — прямоугольный и равнобедренный (\angle QKQ'=45^{\circ}), QQ'=\frac{KQ}{\sqrt2}=\frac{1}{\sqrt{6}}, Q'L^2=QL^2-(QQ')^2=\frac{7}{6}

Q'L — радиус круга, полученного в сечении шара плоскостью \alpha. Тогда площадь сечения равна \pi Q'L^2=\frac76\pi.

б) \frac{7}{6}\pi.