Задание №168
Условие
Правильная треугольная пирамида SABC (ABC — основание) имеет боковое ребро SA=SB=SC=8 и сторону основания AB=BC=AC=12. На середине ребер SB и SC были соответственно взяты точки E и F. Плоскость \alpha, которой принадлежит прямая EF, перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость \alpha делит биссектрису основания пирамиды AA_1 в отношении 5:1, считая от точки A.
б) Вычислите площадь сечения пирамиды SABC плоскостью \alpha.
Решение
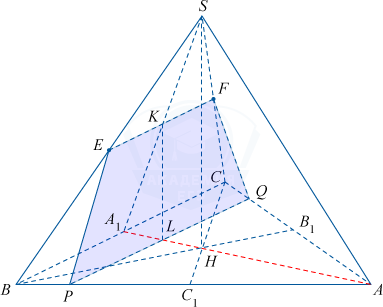
а) EF\parallel BC (как средняя линия \bigtriangleup SBC) \Rightarrow EF\parallel ABC.
Сечение пересекает плоскость основания ABC в некоторой прямой PQ \parallel EF.
Рассмотрим плоскость AA_1S.
Точка K - центр пересечения EF и A_1S, H — центр основания ABC, L – точка пересечения плоскости SAA_1 и прямой PQ.
\begin{cases} PEF \perp ABC \\ SAA_1 \perp ABC \end{cases} \Rightarrow KL \perp ABC, KL \parallel SH
FE — средняя линия \bigtriangleup SBC, A_1K=KS, следовательно, A_1L=LH (т.к. A_1H – проекция прямой A_1S на плоскость основания).
Медиана AA_1 делится точкой H в соотношении: AH:HA_1=2:1\Rightarrow AL:LA_1=5:1, ч.т.д.
б) Рассмотрим трапецию PEFQ.
EF = \frac{1}{2} BC = 12:2 = 6
\frac{PQ}{BC}=\frac{AL}{AA_1}=\frac{5}{6}
PQ=\frac{5BC}{6}=\frac{5\cdot 12}{6}=10
AH=\frac{2}{3} AA_1= \frac{2}{3}\sqrt{AB^2-(\frac{1}{2}AB)^2}= \frac{2}{3}\cdot \frac{\sqrt{3}}{2}AB= \frac{\sqrt{3}\cdot 12}{3}=4\sqrt{3}
KL=\frac{1}{2}SH= \frac{1}{2}\sqrt{SA^2-AH^2}= \frac{1}{2}\sqrt{8^2-(4\sqrt{3})^2}=2
S_{PEFQ}=\frac{1}{2}(EF+PQ)\cdot KL= \frac{1}{2}(6+10)\cdot 2=16
Ответ
16