Задание №959

а) Построим сечение параллелепипеда плоскостью AKF.

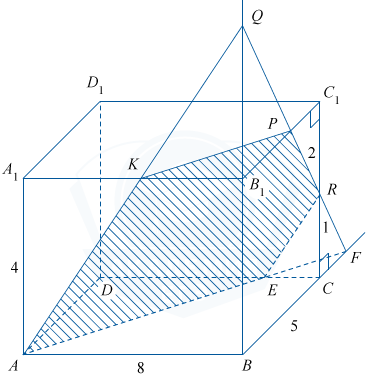
E — точка пересечения ребра DC и отрезка AF.

В плоскости ABB_1 проведем лучи AK и BB_1. AK пересекает BB_1 в точке Q. В плоскости BCC_1 проведем отрезок FQ. FQ пересекает B_1C_1 в точке P, а CC_1 в точке R. Пятиугольник AKPRE — искомое сечение.

KB_1 \parallel AB, KB_1=\frac{1}{2}A_1 B_1, значит KB_1 — средняя линия \bigtriangleup ABQ, отсюда BB_1=QB_1, а так как BF \parallel B_1 P, то B_1 P — средняя линия \bigtriangleup FBQ, BF=8, B_1 P=\frac{1}{2}BF=4. C_1 P=B_1C_1-B_1 P=5-4=1, следовательно, B_1 P:PC_1=4:1.

б) Прямоугольние треугольники ABQ, FBQ и ABF равны по двум катетам AB=BF=BQ=8, отсюда AQ=AF=QF=8\sqrt{2}.

S_{AQF}=\frac{a^{2}\sqrt{3}}{4} как площадь равностороннего треугольника со стороной a.

S_{AQF}=\frac{(8\sqrt{2})^{2} \cdot \sqrt{3}}{4}=32\sqrt{3},

S_{KQP}= \frac{1}{4}S_{AQF}= \frac{32\sqrt{3}}{4}= 8\sqrt{3}.

S_{AKPF}= S_{AQF}-S_{KQP}= 32\sqrt{3}-8\sqrt{3}= 24\sqrt{3}.

\bigtriangleup RCF \sim \bigtriangleup RC_1 P по первому признаку подобия (\angle C=\angle C_1=90^{\circ}, \angle1=\angle2 как вертикальные). Из подобия следует \frac{CF}{PC_{1}}=\frac{FR}{PR}. По доказанному в а) PC_1=1, BF=AB=8, тогда CF=8-5=3 и \frac{FR}{PR}=\frac{3}{1}. Так как KP — средняя линия \bigtriangleup AQF, то PF=\frac{1}{2}QF=4\sqrt{2}, FR=\frac{3PF}{4}=\frac{4\sqrt{2} \cdot 3}{4}=3\sqrt{2}.

В равнобедренном прямоугольном треугольнике FCE FC=EC=3, тогда EF=3\sqrt{2}. В \bigtriangleup REFFR=EF=3\sqrt{2}, \angle RFE=60^{\circ}, отсюда \bigtriangleup REF — равносторонний.S_{REF}=\frac{(3\sqrt{2})^2\sqrt{3}}{4}=\frac{9\sqrt{3}}{2}.

S_{AKPRE}= S_{AKPF}-S_{REF}= 24\sqrt{3}-\frac{9\sqrt{3}}{2}= \frac{39\sqrt{3}}{2}.

\frac{39\sqrt{3}}{2}