Задание №984
Условие
Дана правильная четырёхугольная пирамида SABCD, все рёбра которой равны.
а) Постройте сечение пирамиды плоскостью, проходящей через диагональ BD основания перпендикулярно грани SCD.
б) Найдите площадь этого сечения, если каждое ребро данной пирамиды равно 5.
Решение
а) Пусть K — середина ребра SC. Так как треугольники SDC и SBC равносторонние, то SC \perp DK и SC \perp BK (медиана равностороннего треугольника является его высотой). Значит, прямая SC перпендикулярна плоскости DKB. Так как SC \perp DKB и SC \subset CSD, то плоскость DBK перпендикулярна плоскости CSD. Треугольник DKB — искомое сечение.
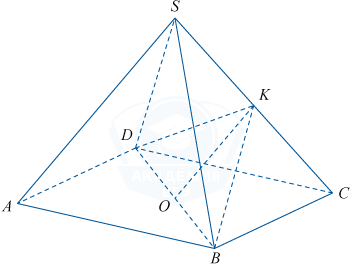
б) Найдём площадь сечения. Высоты DK и BK в равносторонних треугольниках равны \frac{5\sqrt{3}}{2}. Диагональ BD квадрата ABCD равна 5\sqrt{2}. В равнобедренном треугольнике DKB высота OK=\sqrt{\left ( \frac{5\sqrt{3}}{2}\right )^2-\left ( \frac{5\sqrt{2}}{2}\right )^2}=\frac{5}{2}. Площадь треугольника DKB равна \frac{1}{2}DB \cdot OK=\frac{1}{2} \cdot 5\sqrt{2} \cdot \frac{5}{2}=\frac{25\sqrt{2}}{4}.
Ответ
\frac{25\sqrt{2}}{4}.
Даша Матросова /