Задание №1185
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 сторона основания равна 9, боковое ребро равно 14. Точка K принадлежит ребру A_1B_1 и делит его в отношении 2:7, считая от вершины A_1.
а) Докажите, что сечение призмы плоскостью, проходящей через точки A, C и K, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Решение
а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL \parallel AC. Следовательно, искомым сечением будет трапеция AKLC.
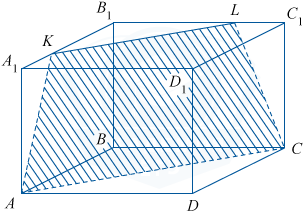
KB_1\parallel AB, B_1L\parallel BC, KL\parallel AC. Значит, треугольники KB_1L и ABC подобны и являются равнобедренными прямоугольными треугольниками. Тогда KB_1=B_1L и A_1K=C_1L. Треугольники AA_1K и CC_1L равны, следовательно, AK=CL и трапеция AKLC — равнобедренная.
б) Найдём площадь трапеции AKLC.
A_1K=\frac29A_1B_1 =\frac29\cdot 9=2.
Из \triangle AA_1K,\, AK = \sqrt {AA_1^2+A_1K^2}= \sqrt {14^2+2^2}= 10\sqrt 2.
AC=AB\sqrt 2=9\sqrt 2; KL =\frac79AC=\frac79\cdot 9\sqrt 2=7\sqrt 2.
Так как трапеция AKLC — равнобедренная, имеем
AH =\frac{AC-KL}2=\sqrt 2.
Из \triangle AKH,\, KH= \sqrt {AK^2-AH^2}= \sqrt {200-2}= \sqrt {198}.
S_{AKLC}=\frac{AC+KL}2\cdot KH\,= 8\sqrt 2\cdot \sqrt {198}=48\sqrt {11}.
Ответ
48\sqrt {11}.