Задание №1186
Условие
В правильном тетраэдре DABC с ребром 5 на рёбрах AD, BD и AC выбраны точки K, L и M соответственно так, что KD=MC=2, LD=4.
а) Постройте сечение тетраэдра плоскостью KLM.
б) Найдите площадь этого сечения.
Решение
а) Так как AK=AM=5-2=3, то \triangle AKM равнобедренный.
.png)
Так как в этом равнобедренном треугольнике \angle KAM=60^{\circ}, то он равносторонний, то есть
KM=3. Тогда KM \parallel DC, так как равны соответственные углы при прямых KM, DC и секущей AD.
Построим LN \parallel DC. Так как в этом случае LN \parallel KM, то точки K, L, N и M лежат в одной плоскости, то есть трапеция KLNM есть искомое сечение.
б) 1. \triangle BLN \sim \triangle BDC, так как LN \parallel DC. Следовательно, \triangle BLN является равносторонним и LN=BN=BL =BD-LD=5-4=1.
2. \triangle DKL=\triangle CMN, так как DK=CM =2, DL=CN=4 и \angle KDL=\angle MCN=60^{\circ}. Значит, KL=MN и KMNL — равнобедренная трапеция.
Опустим в ней высоту LH. Отсюда, KH =\frac{KM-LN}2=\frac{3-1}2=1.
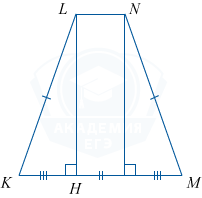
3. По теореме косинусов для \triangle KDL получим:
KL^2= KD^2+DL^2-2\cdot KD\cdot DL\cdot \cos 60^{\circ}= 2^2+4^2-2\cdot 2\cdot 4\cdot \frac12= 12.
4. По теореме Пифагора LH= \sqrt {KL^2-KH^2}= \sqrt {12-1}= \sqrt {11}.
5. S_{KMNL}= \frac12(KM+LN)\cdot LH= \frac12(3+1)\cdot \sqrt {11}= 2\sqrt {11}.
Ответ
2\sqrt {11}.