Задания по теме «Окружность»

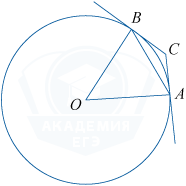
Центральный угол равен угловой величине дуги, на которую он опирается, то есть

\angle BOA = 56^{\circ}. Углы OBC и OAC прямые как углы между касательными и радиусами, проведёнными в точки касания. Сумма углов четырёхугольника равна 360^{\circ}, можем найти угол ACB.

\angle ACB = 360^{\circ}-56^{\circ}-90^{\circ}-90^{\circ} = 124^{\circ}.

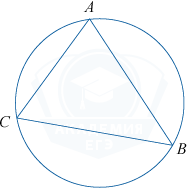
Угловая величина всей окружности составляет 360^{\circ}, дуги, на которые опираются углы треугольника, составляют 2, 3 и 4 из 2 + 3 + 4 = 9 частей, то есть большая из них равна \frac49 окружности, 360^{\circ}\cdot\frac49=160^{\circ}. Вписанный угол равен половине дуги, на которую он опирается, то есть 160^{\circ} : 2 = 80^{\circ}.

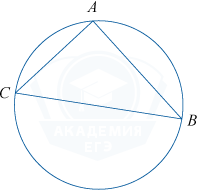
Угловая величина всей окружности составляет 360^{\circ}, дуга, на которую опирается угол C, составляет 7 из 7+13 = 20 частей, то есть \frac{7}{20} окружности, 360^{\circ}\cdot \frac{7}{20} = 126^{\circ}. Вписанный угол равен половине дуги, на которую он опирается, то есть 126^{\circ} : 2 = 63^{\circ}.

Угловая величина всей окружности составляет 360^{\circ}, дуга составляет треть окружности, то есть 360^{\circ}:3=120^{\circ}. Вписанный угол равен половине дуги, на которую он опирается, то есть 120^{\circ}:2=60^{\circ}.

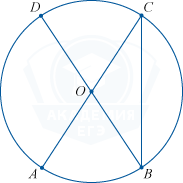
Так как угол ACB вписан в окружность, то градусная мера дуги AB, на которую он опирается, в 2 раза больше величине этого угла, и равна:

\cup AB=2\cdot\angle ACB=2\cdot21^{\circ}=42^{\circ}

Так как BD — диаметр окружности, то его градусная мера равна 180^{\circ}. Найдем градусную меру угла дуги AD:

\cup AD=180^{\circ}-\cup AB=180^{\circ}-42^{\circ}=138^{\circ}

Так как угол AOD — центральный, то его величина равна градусной мере дуги окружности AD, следовательно:

\angle AOD=\cup AD=138^{\circ}

Угол DAE мы можем найти зная два остальных угла треугольника ACD. Угол ACB нам известен и равен углу ACD. Угол ADC является разностью развернутого угла BDC и угла ADB. Угол ADB является вписанным в окружность, а значит его величина равна половине градусной меры дуги, на которую он опирается.

Из условия задачи градусная мера дуги AB известна. Найдем угол ADB:

\angle ADB=138^{\circ}:2=69^{\circ}

Найдем угол ADC:

\angle ADC=180^{\circ}-\angle ADB=180^{\circ}-69^{\circ}=111^{\circ}

Угол DAE равен углу DAC. Зная два угла треугольника, найдем искомый угол DAE:

\angle DAE=180^{\circ}-\angle ADC-\angle ACD=180^{\circ}-111^{\circ}-54^{\circ}=15^{\circ}

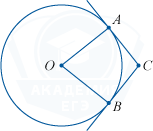
Прямые CA и CB являются касательными к окружности, значит они образуют прямой угол с радиусом окружности, то есть с прямыми OA и OB. Сумма углов четырехугольника равна 360^{\circ}. Найдем неизвестный угол ACB:

\angle ACB=360^{\circ}-2\cdot 90^{\circ}-64^{\circ}=116^{\circ}

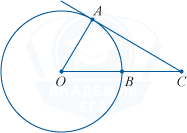
Прямая AC является касательной к окружности, значит радиус AO образует с ней прямой угол, следовательно треугольник AOC прямоугольный. Величину меньшей дуги окружности AB вы можем найти зная градусную меру угла AOB. Учитывая, что сумма углов треугольника равна 180^{\circ}, найдем угол AOB:

\angle AOB = 180^{\circ}-90^{\circ}-27^{\circ} = 63^{\circ}

Так как угол AOB – центральный, то величина меньшей дуги окружности AB равна градусной мере этого угла, а значит величина дуги равна 63^{\circ}