Задание №1069

Тип задания: 6
Тема: Окружность

Условие

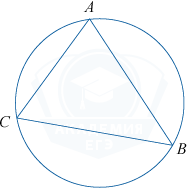
Точки A, B, C, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как 2:3:4. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Окружность, разделенная точками на три дуги

Показать решение

Решение

Угловая величина всей окружности составляет 360^{\circ}, дуги, на которые опираются углы треугольника, составляют 2, 3 и 4 из 2 + 3 + 4 = 9 частей, то есть большая из них равна \frac49 окружности, 360^{\circ}\cdot\frac49=160^{\circ}. Вписанный угол равен половине дуги, на которую он опирается, то есть 160^{\circ} : 2 = 80^{\circ}.