Задание №1070
Условие
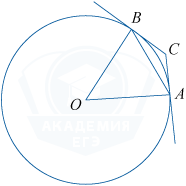
Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна 56^{\circ}. Найдите угол ACB. Ответ дайте в градусах.
Решение
Центральный угол равен угловой величине дуги, на которую он опирается, то есть
\angle BOA = 56^{\circ}. Углы OBC и OAC прямые как углы между касательными и радиусами, проведёнными в точки касания. Сумма углов четырёхугольника равна 360^{\circ}, можем найти угол ACB.
\angle ACB = 360^{\circ}-56^{\circ}-90^{\circ}-90^{\circ} = 124^{\circ}.
Ответ
124
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.