Открытый банк заданий по теме треугольник общего вида. Задания B6 из ЕГЭ по математике (профильный уровень)
Найдите площадь треугольника, две стороны которого равны 6 и 14, а угол между ними равен 30^{\circ}.
Площадь треугольника можно найти как половину произведения двух его сторон на синус угла между ними. В заданном треугольнике площадь S= \frac12\cdot6\cdot14\cdot\sin30^{\circ}= 21.
В тупоугольном треугольнике ABC AC=BC=50, AH — высота, CH=40. Найдите \cos ACB.
\angle ACB=180^{\circ}-\angle ACH, поэтому \cos\angle ACB=-\cos\angle ACH=-\frac{CH}{AC}.
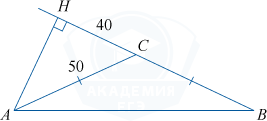
По условию CH=40, AC=50.
\cos\angle ACB=-\frac{40}{50}=-0,8
В треугольнике ABC угол A равен 48^{\circ}, угол C равен 62^{\circ}. На продолжении стороны AB за точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
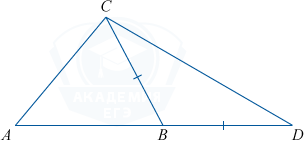
Угол CBD является внешним углом треугольника ABC и равен сумме двух углов треугольника, не смежных с ним. Найдём угол CBD.
\angle CBD = \angle A + \angle C = 48^{\circ}+62^{\circ}= 110^{\circ}. Треугольник BCD равнобедренный, его углы при основании равны: \angle D=\angle DCB. Сумма углов треугольника равна 180^{\circ}. Тогда \angle D = (180^{\circ}-110^{\circ}):2=35^{\circ}.
К сторонам треугольника равным 12 и 8 проведены высоты. Высота, проведенная к первой стороне, равна 4. Найдите длину высоты, проведенной ко второй стороне.
По условию задачи AB=12, BC=8, CH=4.
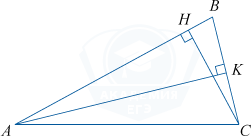
Найдем площадь треугольника ABC.
S_{ABC}=\frac{AB\cdot CH}{2}=\frac{12\cdot4}{2}=24.
С другой стороны, S_{ABC}=\frac{BC\cdot AK}{2}=\frac{8\cdot AK}{2}=24, откуда AK=6.
В тупоугольном треугольнике ABC\:AC=BC=15, высота AH равна 12. Найдите \sin\angle ACB.
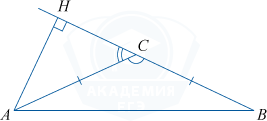
В прямоугольном \triangle ACH\:\sin\angle ACH=\frac{AH}{AC}=\frac{12}{15}=\frac45.
Тогда \sin \angle ACB= \sin(\pi-\angle ACH)= \sin\angle ACH= \frac45= 0,8.
В треугольнике ABC угол С равен 91^{\circ}, угол А равен 41^{\circ}. Найдите внешний угол треугольника при вершине B.
.png)
Так как сумма углов треугольника равна 180 градусов, то внутренний угол при вершине B будет равен: 180^{\circ} - \angle A - \angle C = 180^{\circ} - 41^{\circ} - 91^{\circ} = 48^{\circ}
Значит искомый внешний угол будет равен: 180^{\circ} - 48^{\circ} = 132^{\circ}
В треугольнике ABC биссектрисы AD и BE пересекаются в точке O. Угол C равен 32^{\circ}. Найдите угол AOB. Ответ дайте в градусах.
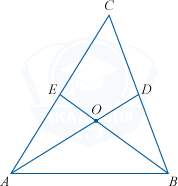
Учитывая, что сумма углов треугольника равна 180 градусам, справедливо уравнение:
\angle BAC + \angle ABC + \angle ACB = 180^{\circ}
Т.к. биссектриса делит угол пополам, то:
\angle BAC = 2 \cdot \angle BAO и \angle ABC = 2 \cdot \angle ABO.
Отсюда получим:
2 \cdot \angle BAO + 2 \cdot \angle ABO + 32^{\circ} = 180^{\circ}
\angle BAO + \angle ABO + 16^{\circ} = 90^{\circ}
\angle BAO + \angle ABO = 74^{\circ}
Зная, что сумма углов BAO и ABO равна 74^{\circ}, найдем искомый угол AOB:
\angle AOB = 180^{\circ} - 74^{\circ} = 106^{\circ}
Закажите обратный звонок!