Задание №889
Условие
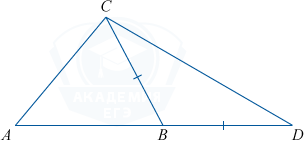
В треугольнике ABC угол A равен 48^{\circ}, угол C равен 62^{\circ}. На продолжении стороны AB за точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
Решение
Угол CBD является внешним углом треугольника ABC и равен сумме двух углов треугольника, не смежных с ним. Найдём угол CBD.
\angle CBD = \angle A + \angle C = 48^{\circ}+62^{\circ}= 110^{\circ}. Треугольник BCD равнобедренный, его углы при основании равны: \angle D=\angle DCB. Сумма углов треугольника равна 180^{\circ}. Тогда \angle D = (180^{\circ}-110^{\circ}):2=35^{\circ}.
Ответ
35
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.