Задания по теме «Область допустимых значений (ОДЗ)»

а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 \sin x-2 \cos x-tg x=0. Учитывая, что \cos x \neq 0, слагаемое 2 \sin x можно заменить на 2 tg x \cos x, получим уравнение 1+2 tg x \cos x-2 \cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 \cos x)=0.

1) 1-tg x=0,  tg x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;

2) 1-2 \cos x=0,  \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.

б) С помощью числовой окружности отберём корни, принадлежащие промежутку \left[ \frac{3\pi }2;\, 3\pi \right].

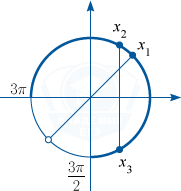
x_1=\frac\pi 4+2\pi =\frac{9\pi }4,

x_2=\frac\pi 3+2\pi =\frac{7\pi }3,

x_3=-\frac\pi 3+2\pi =\frac{5\pi }3.

а) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;

б) \frac{5\pi }3,  \frac{7\pi }3,  \frac{9\pi }4.

а) ОДЗ: \begin{cases} tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end{cases}

Исходное уравнение на ОДЗ равносильно совокупности уравнений

\left[\!\!\begin{array}{l} 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end{array}\right.

Решим первое уравнение. Для этого сделаем замену \cos 4x=t,  t \in [-1; 1]. Тогда \sin^24x=1-t^2. Получим:

2(1-t^2)-3t=0,

2t^2+3t-2=0,

t_1=\frac12, t_2=-2, t_2\notin [-1; 1].

\cos 4x=\frac12,

4x=\pm \frac\pi 3+2\pi n,

x=\pm \frac\pi {12}+\frac{\pi n}2, n \in \mathbb Z.

Решим второе уравнение.

tg x=0,\, x=\pi k, k \in \mathbb Z.

При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.

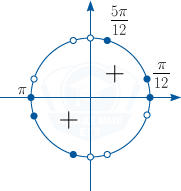
Знаком «+» отмечены 1-я и 3-я четверти, в которых tg x>0.

Получим: x=\pi k, k \in \mathbb Z; x=\frac\pi {12}+\pi n, n \in \mathbb Z; x=\frac{5\pi }{12}+\pi m, m \in \mathbb Z.

б) Найдём корни, принадлежащие промежутку \left( 0;\,\frac{3\pi }2\right].

x=\frac\pi {12}, x=\frac{5\pi }{12}; x=\pi ; x=\frac{13\pi }{12}; x=\frac{17\pi }{12}.

а) \pi k, k \in \mathbb Z; \frac\pi {12}+\pi n, n \in \mathbb Z; \frac{5\pi }{12}+\pi m, m \in \mathbb Z.

б) \pi; \frac\pi {12}; \frac{5\pi }{12}; \frac{13\pi }{12}; \frac{17\pi }{12}.

а) Так как \sin \frac\pi 3=\cos \frac\pi 6, то \sin ^2\frac\pi 3=\cos ^2\frac\pi 6, значит, заданное уравнение равносильно уравнению \cos^2x=\cos ^22x, которое, в свою очередь, равносильно уравнению \cos^2x-\cos ^2 2x=0.

Но \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x) и

\cos 2x=2 \cos ^2 x-1, поэтому уравнение примет вид

(\cos x-(2 \cos ^2 x-1))\,\cdot (\cos x+(2 \cos ^2 x-1))=0,

(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.

Тогда либо 2 \cos ^2 x-\cos x-1=0, либо 2 \cos ^2 x+\cos x-1=0.

Решая первое уравнение как квадратное уравнение относительно \cos x, получаем:

(\cos x)_{1,2}=\frac{1\pm\sqrt 9}4=\frac{1\pm3}4. Поэтому либо \cos x=1, либо \cos x=-\frac12. Если \cos x=1, то x=2k\pi , k \in \mathbb Z. Если \cos x=-\frac12, то x=\pm \frac{2\pi }3+2s\pi , s \in \mathbb Z.

Аналогично, решая второе уравнение, получаем либо \cos x=-1, либо \cos x=\frac12.Если \cos x=-1, то корни x=\pi +2m\pi , m \in \mathbb Z. Если \cos x=\frac12, то x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.

Объединим полученные решения:

x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.

б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.

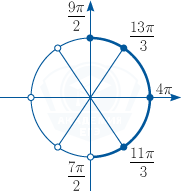
Получим: x_1 =\frac{11\pi }3,  x_2=4\pi ,  x_3 =\frac{13\pi }3.

а) m\pi, m \in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;

б) \frac{11\pi }3,  4\pi ,  \frac{13\pi }3.

а) 1. Согласно формуле приведения, ctg\left( \frac{3\pi }2-x\right) =tgx. Областью определения уравнения будут такие значения x, что \cos x \neq 0 и tg x \neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 \cos ^2 \frac x2=1+\cos x. Получим уравнение: 5(1+\cos x) =\frac{11+5tgx}{1+tgx}.

Заметим, что \frac{11+5tgx}{1+tgx}= \frac{5(1+tgx)+6}{1+tgx}= 5+\frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 \cos x=5 +\frac{6}{1+tgx}. Отсюда \cos x =\frac{\dfrac65}{1+tgx}, \cos x+\sin x =\frac65.

2. Преобразуем \sin x+\cos x по формуле приведения и формуле суммы косинусов: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left( x-\frac\pi 4\right) = \frac65.

Отсюда \cos \left(x-\frac\pi 4\right) =\frac{3\sqrt 2}5. Значит, x-\frac\pi 4= arc\cos \frac{3\sqrt 2}5+2\pi k, k \in \mathbb Z,

или x-\frac\pi 4= -arc\cos \frac{3\sqrt 2}5+2\pi t, t \in \mathbb Z.

Поэтому x=\frac\pi 4+arc\cos \frac{3\sqrt 2}5+2\pi k,k \in \mathbb Z,

или x =\frac\pi 4-arc\cos \frac{3\sqrt 2}5+2\pi t,t \in \mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=\frac\pi 4+arccos \frac{3\sqrt 2}5 и b=\frac\pi 4-arccos \frac{3\sqrt 2}5.

1. Докажем вспомогательное неравенство:

\frac{\sqrt 2}{2}<\frac{3\sqrt 2}2<1.

Действительно, \frac{\sqrt 2}{2}=\frac{5\sqrt 2}{10}<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Заметим также, что \left( \frac{3\sqrt 2}5\right) ^2=\frac{18}{25}<1^2=1, значит \frac{3\sqrt 2}5<1.

2. Из неравенств (1) по свойству арккосинуса получаем:

arccos 1<arc\cos \frac{3\sqrt 2}5<arc\cos \frac{\sqrt 2}2,

0<arccos\frac{3\sqrt2}{5}<\frac{\pi}{4}.

Отсюда \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

0<a<\frac\pi 2.

Аналогично, -\frac\pi 4<arccos\frac{3\sqrt2}{5}<0,

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

0<b<\frac\pi 2.

При k=-1 и t=-1 получаем корни уравнения a-2\pi и b-2\pi.

\Bigg( a-2\pi =-\frac74\pi +arccos \frac{3\sqrt 2}5,\, b-2\pi =-\frac74\pi -arccos \frac{3\sqrt 2}5\Bigg). При этом -2\pi <a-2\pi <-\frac{3\pi }2,

-2\pi <b-2\pi <-\frac{3\pi }2. Значит, эти корни принадлежат заданному промежутку \left( -2\pi , -\frac{3\pi }2\right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если k\geqslant 1 и t\geqslant 1, то корни больше 2\pi. Если k\leqslant -2 и t\leqslant -2, то корни меньше -\frac{7\pi }2.

а) \frac\pi4\pm arccos\frac{3\sqrt2}5+2\pi k, k\in\mathbb Z;

б) -\frac{7\pi}4\pm arccos\frac{3\sqrt2}5.

а) Преобразуем уравнение:

\cos x =-\sin 2x,

\cos x+2 \sin x \cos x=0,

\cos x(1+2 \sin x)=0,

\cos x=0,

x =\frac\pi 2+\pi n, n \in \mathbb Z;

1+2 \sin x=0,

\sin x=-\frac12,

x=(-1)^{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z.

б) Корни, принадлежащие отрезку [0; \pi ], найдём с помощью единичной окружности.

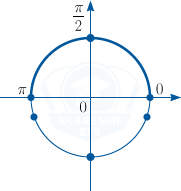
Указанному промежутку принадлежит единственное число \frac\pi 2.

а) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z;

б) \frac\pi 2.

а) Найдём ОДЗ уравнения: \cos 2x \neq -1, \cos (\pi +x) \neq -1; Отсюда ОДЗ: x \neq \frac \pi 2+\pi k,

k \in \mathbb Z, x \neq 2\pi n, n \in \mathbb Z. Заметим, что при \sin x=1, x=\frac \pi 2+2\pi k, k \in \mathbb Z.

Полученное множество значений x не входит в ОДЗ.

Значит, \sin x \neq 1.

Разделим обе части уравнения на множитель (\sin x-1), отличный от нуля. Получим уравнение \frac 1{1+\cos 2x}=\frac 1{1+\cos (\pi +x)}, или уравнение 1+\cos 2x=1+\cos (\pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 \cos ^2 x=1-\cos x. Это уравнение с помощью замены \cos x=t, где -1 \leqslant t \leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=\frac12. Возвращаясь к переменной x, получим \cos x = \frac12 или \cos x=-1, откуда x=\frac \pi 3+2\pi m, m \in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z.

б) Решим неравенства

1) -\frac{3\pi }2 \leqslant \frac{\pi }3+2\pi m \leqslant -\frac \pi 2 ,

2) -\frac{3\pi }2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi {2,}

3) -\frac{3\pi }2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2 , m, n, k \in \mathbb Z. 

Решение:

1) -\frac{3\pi }2 \leqslant \frac{\pi }3+2\pi m \leqslant -\frac \pi 2 , -\frac32 \leqslant  \frac13+2m \leqslant  -\frac12 -\frac{11}6 \leqslant  2m \leqslant  -\frac56 , -\frac{11}{12} \leqslant m \leqslant -\frac5{12}.

Нет целых чисел, принадлежащих промежутку \left [-\frac{11}{12};-\frac5{12}\right].

2) -\frac {3\pi} 2 \leqslant -\frac{\pi }3+2\pi n \leqslant -\frac{\pi }{2}, -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12 , -\frac76 \leqslant 2n \leqslant -\frac1{6}, -\frac7{12} \leqslant n \leqslant -\frac1{12}.

Нет целых чисел, принадлежащих промежутку \left[ -\frac7{12} ; -\frac1{12} \right].

3) -\frac{3\pi }2 \leqslant \pi +2\pi k\leqslant -\frac{\pi }2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34.

Этому неравенству удовлетворяет k=-1, тогда x=-\pi.

а) \frac \pi 3+2\pi m; -\frac \pi 3+2\pi n; \pi +2\pi k, m, n, k \in \mathbb Z;

б) -\pi .

а) Так как \sin \frac\pi 6=\cos \frac\pi 3, то \sin ^2\frac\pi 6=\cos ^2\frac\pi 3, значит, заданное уравнение равносильно уравнению \sin ^2 x=\cos ^2 2x, которое, в свою очередь, равносильно уравнению \sin ^2- \cos ^2 2x=0.

Но \sin ^ 2x-\cos ^2 2x= (\sin x-\cos 2x)\cdot (\sin x+\cos 2x) и

\cos 2x=1-2 \sin ^2 x, поэтому уравнение примет вид

(\sin x-(1-2 \sin ^2 x))\,\cdot (\sin x+(1-2 \sin ^2 x))=0,

(2 \sin ^2 x+\sin x-1)\,\cdot (2 \sin ^2 x-\sin x-1)=0.

Тогда либо 2 \sin ^2 x+\sin x-1=0, либо 2 \sin ^2 x-\sin x-1=0.

Решим первое уравнение как квадратное относительно \sin x,

(\sin x)_{1,2}=\frac{-1 \pm \sqrt 9}4=\frac{-1 \pm 3}4. Поэтому либо \sin x=-1, либо \sin x=\frac12. Если \sin x=-1, то x=\frac{3\pi }2+ 2k\pi , k \in \mathbb Z. Если \sin x=\frac12, то либо x=\frac\pi 6 +2s\pi , s \in \mathbb Z, либо x=\frac{5\pi }6+2t\pi , t \in \mathbb Z.

Аналогично, решая второе уравнение, получаем либо \sin x=1, либо \sin x=-\frac12. Тогда x =\frac\pi 2+2m\pi , m \in \mathbb Z, либо x=\frac{-\pi }6 +2n\pi , n \in \mathbb Z, либо x=\frac{-5\pi }6+2p\pi , p \in \mathbb Z.

Объединим полученные решения:

x=\frac\pi 2+m\pi,m\in\mathbb Z; x=\pm\frac\pi 6+s\pi,s \in \mathbb Z.

б) Выберем корни, которые попали в заданный промежуток с помощью числовой окружности.

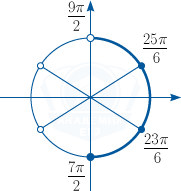
Получим: x_1 =\frac{7\pi }2, x_2 =\frac{23\pi }6, x_3 =\frac{25\pi }6.

а) \frac\pi 2+ m\pi , m \in \mathbb Z; \pm \frac\pi 6 +s\pi , s \in \mathbb Z;

б) \frac{7\pi }2;\,\,\frac{23\pi }6;\,\,\frac{25\pi }6.

а) Так как \cos \frac{5\pi }4= \cos \left( \pi +\frac\pi 4\right) = -\cos \frac\pi 4= -\frac{\sqrt 2}2 и \cos \frac{3\pi }4= \cos \left( \pi -\frac\pi 4\right) = -\cos \frac\pi 4= -\frac{\sqrt 2}2, то уравнение примет вид: 2\cos x\left( \cos x-\frac{\sqrt 2}2\right) +\cos x-\frac{\sqrt 2}2=0.Отсюда (2\cos x+1)\left( \cos x-\frac{\sqrt 2}2\right) =0.

Тогда \cos x=-\frac12; x=\pm\frac{2\pi }3+2\pi n или \cos x=\frac{\sqrt 2}2;\, x=\pm\frac\pi 4+2\pi n, где n \in \mathbb Z.

б) Корни, принадлежащие промежутку \left[ \pi ;\,\frac{5\pi }2\right), найдём с помощью числовой окружности: \frac{4\pi }3;\,\, \frac{7\pi }4;\,\, \frac{9\pi }4.

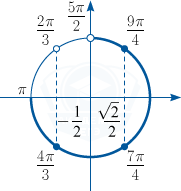
а) \pm\frac{2\pi }3+2\pi n;\,\, \pm\frac\pi 4=2\pi n, n \in \mathbb Z.

б) \frac{4\pi }3;\, \frac{7\pi }4;\, \frac{9\pi }4.

а) После замены t=\log_2\left( \frac{\sin x}{2}\right) исходное уравнение примет вид 2t^2-7t-15=0. Корни этого уравнения t=\frac{-3}{2}, t=5. Возвращаясь к переменной x, получим:

\left[\!\!\begin{array}{l} \log_2\left( \frac{\sin x}{2}\right) =5, \\ \log_2\left( \frac{\sin x}{2}\right) =\frac{-3}{2}; \end{array}\right. \left[\!\!\begin{array}{l} \frac{\sin x}{2} =2^5, \\ \frac{\sin x}{2} =\frac{1}{2\sqrt 2}. \end{array}\right.

Первое уравнение совокупности не имеет корней. Решая второе уравнение, получим:

x=(-1)^n\frac\pi 4+\pi n, n \in \mathbb Z.

б) Запишем решение уравнения в виде x =\frac\pi 4+2\pi n, n \in \mathbb Z или x=\frac{3\pi }{4}+2\pi k, k \in \mathbb Z и выясним, для каких целых значений n и k справедливы неравенства \frac\pi 2\leqslant \frac\pi 4+2\pi n\leqslant 3\pi и \frac\pi 2\leqslant \frac{3\pi }{4}+2\pi k\leqslant 3\pi.

Получим: \frac18\leqslant n\leqslant \frac{11}{8} и -\frac18\leqslant k\leqslant \frac98, откуда следует, что n=1, k=0, k=1.

При n=1\enspace x=\frac\pi 4+2\pi\cdot 1=\frac{9\pi}4.

При k=0\enspace x=\frac{3\pi }{4}.

При k=1\enspace x=\frac{3\pi }{4}+2\pi\cdot 1=\frac{11\pi }{4}.

Итак, \frac{3\pi }{4}, \frac{9\pi }{4}, \frac{11\pi }{4} — корни уравнения, принадлежащие промежутку \left[ \frac\pi 2; 3\pi \right].

а) (-1)^n\frac\pi 4+\pi n, n \in \mathbb Z;

б) \frac{3\pi }{4}, \frac{9\pi }{4}, \frac{11\pi }{4}

а) Преобразуем уравнение, согласно формуле приведения

\cos \left ( x+\frac{\pi}{2}\right )=-\sin x:

2\cos^2 x+5\cos x+2=0.

Обозначим \cos x=t, -1 \leq t \leq 1, получим 2t^2+5t+2=0.

t_{1}=\frac{-5-3}{2 \cdot 2}=-2 — не удовлетворяет условию -1 \leq t \leq 1.

t_{2}=\frac{-5+3}{2 \cdot 2}=-\frac{1}{2}.

Вернёмся к исходной переменной:

\cos x=-\frac{1}{2},

x=\pm \left ( \pi - \frac{\pi}{3}\right )+2\pi n, n \in \mathbb Z,

x=\pm \frac{2\pi}{3}+2\pi n, n \in \mathbb Z.

б) Корни, принадлежащие промежутку \left [\frac{\pi}{2}; \frac{3\pi}{2} \right ], найдём с помощью единичной окружности.

Получаем числа \frac{2\pi}{3};\frac{4\pi}{3}.

а) \pm \frac{2\pi}{3}+2\pi n, n \in \mathbb Z;

б) \frac{2\pi}{3}, \frac{4\pi}{3}