Задание №1178

а) ОДЗ: \begin{cases} tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end{cases}

Исходное уравнение на ОДЗ равносильно совокупности уравнений

\left[\!\!\begin{array}{l} 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end{array}\right.

Решим первое уравнение. Для этого сделаем замену \cos 4x=t,  t \in [-1; 1]. Тогда \sin^24x=1-t^2. Получим:

2(1-t^2)-3t=0,

2t^2+3t-2=0,

t_1=\frac12, t_2=-2, t_2\notin [-1; 1].

\cos 4x=\frac12,

4x=\pm \frac\pi 3+2\pi n,

x=\pm \frac\pi {12}+\frac{\pi n}2, n \in \mathbb Z.

Решим второе уравнение.

tg x=0,\, x=\pi k, k \in \mathbb Z.

При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.

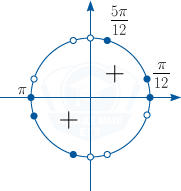
Знаком «+» отмечены 1-я и 3-я четверти, в которых tg x>0.

Получим: x=\pi k, k \in \mathbb Z; x=\frac\pi {12}+\pi n, n \in \mathbb Z; x=\frac{5\pi }{12}+\pi m, m \in \mathbb Z.

б) Найдём корни, принадлежащие промежутку \left( 0;\,\frac{3\pi }2\right].

x=\frac\pi {12}, x=\frac{5\pi }{12}; x=\pi ; x=\frac{13\pi }{12}; x=\frac{17\pi }{12}.

а) \pi k, k \in \mathbb Z; \frac\pi {12}+\pi n, n \in \mathbb Z; \frac{5\pi }{12}+\pi m, m \in \mathbb Z.

б) \pi; \frac\pi {12}; \frac{5\pi }{12}; \frac{13\pi }{12}; \frac{17\pi }{12}.