Задание №1179

а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 \sin x-2 \cos x-tg x=0. Учитывая, что \cos x \neq 0, слагаемое 2 \sin x можно заменить на 2 tg x \cos x, получим уравнение 1+2 tg x \cos x-2 \cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 \cos x)=0.

1) 1-tg x=0,  tg x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;

2) 1-2 \cos x=0,  \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.

б) С помощью числовой окружности отберём корни, принадлежащие промежутку \left[ \frac{3\pi }2;\, 3\pi \right].

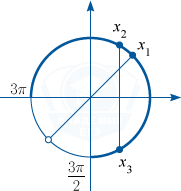
x_1=\frac\pi 4+2\pi =\frac{9\pi }4,

x_2=\frac\pi 3+2\pi =\frac{7\pi }3,

x_3=-\frac\pi 3+2\pi =\frac{5\pi }3.

а) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;

б) \frac{5\pi }3,  \frac{7\pi }3,  \frac{9\pi }4.