Задание №1173

а) Так как \sin \frac\pi 6=\cos \frac\pi 3, то \sin ^2\frac\pi 6=\cos ^2\frac\pi 3, значит, заданное уравнение равносильно уравнению \sin ^2 x=\cos ^2 2x, которое, в свою очередь, равносильно уравнению \sin ^2- \cos ^2 2x=0.

Но \sin ^ 2x-\cos ^2 2x= (\sin x-\cos 2x)\cdot (\sin x+\cos 2x) и

\cos 2x=1-2 \sin ^2 x, поэтому уравнение примет вид

(\sin x-(1-2 \sin ^2 x))\,\cdot (\sin x+(1-2 \sin ^2 x))=0,

(2 \sin ^2 x+\sin x-1)\,\cdot (2 \sin ^2 x-\sin x-1)=0.

Тогда либо 2 \sin ^2 x+\sin x-1=0, либо 2 \sin ^2 x-\sin x-1=0.

Решим первое уравнение как квадратное относительно \sin x,

(\sin x)_{1,2}=\frac{-1 \pm \sqrt 9}4=\frac{-1 \pm 3}4. Поэтому либо \sin x=-1, либо \sin x=\frac12. Если \sin x=-1, то x=\frac{3\pi }2+ 2k\pi , k \in \mathbb Z. Если \sin x=\frac12, то либо x=\frac\pi 6 +2s\pi , s \in \mathbb Z, либо x=\frac{5\pi }6+2t\pi , t \in \mathbb Z.

Аналогично, решая второе уравнение, получаем либо \sin x=1, либо \sin x=-\frac12. Тогда x =\frac\pi 2+2m\pi , m \in \mathbb Z, либо x=\frac{-\pi }6 +2n\pi , n \in \mathbb Z, либо x=\frac{-5\pi }6+2p\pi , p \in \mathbb Z.

Объединим полученные решения:

x=\frac\pi 2+m\pi,m\in\mathbb Z; x=\pm\frac\pi 6+s\pi,s \in \mathbb Z.

б) Выберем корни, которые попали в заданный промежуток с помощью числовой окружности.

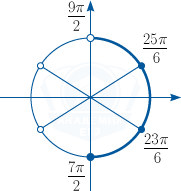
Получим: x_1 =\frac{7\pi }2, x_2 =\frac{23\pi }6, x_3 =\frac{25\pi }6.

а) \frac\pi 2+ m\pi , m \in \mathbb Z; \pm \frac\pi 6 +s\pi , s \in \mathbb Z;

б) \frac{7\pi }2;\,\,\frac{23\pi }6;\,\,\frac{25\pi }6.