Задание №1175
Условие
а) Решите уравнение \sin \left( \frac\pi 2+x\right) =\sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; \pi ];
Решение
а) Преобразуем уравнение:
\cos x =-\sin 2x,
\cos x+2 \sin x \cos x=0,
\cos x(1+2 \sin x)=0,
\cos x=0,
x =\frac\pi 2+\pi n, n \in \mathbb Z;
1+2 \sin x=0,
\sin x=-\frac12,
x=(-1)^{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z.
б) Корни, принадлежащие отрезку [0; \pi ], найдём с помощью единичной окружности.
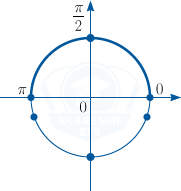
Указанному промежутку принадлежит единственное число \frac\pi 2.
Ответ
а) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z;
б) \frac\pi 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.