Открытый банк заданий по теме трапеция. Задания B6 из ЕГЭ по математике (профильный уровень)
Большее основание равнобедренной трапеции равно 24. Боковая сторона равна 7. Синус острого угла равен \frac{\sqrt{33}}{7}. Найдите меньшее основание.
Рассмотрим равнобедренную трапецию ABCD, в которой BC и AD — основания, AD = 24, AB = CD = 7. Проведём высоты CK и BH. BCKH — прямоугольник, BC = KH.
.png)
Треугольник ABH прямоугольный, \cos A = \frac{AH}{AB}. Вычислим \cos A= \sqrt{1-\sin^2A}= \sqrt{1-\left (\frac{\sqrt{33}}{7}\right)^2}= \frac47. AH= AB\cos A= 7\cdot\frac47= 4. Треугольники ABH и DCK равны по гипотенузе и острому угу, откуда AH=KD=4, BC=24-4-4=16.
Площадь треугольника МРЕ равна 68, KT — средняя линия, параллельная стороне MP. Найдите площадь трапеции MPTK.
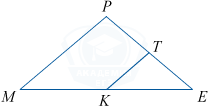
S_{MPTK}=S_{MPE}-S_{KTE}. KT — средняя линия, параллельная стороне MP, поэтому K и T — середины сторон и ET=\frac12EP, KE=\frac12 EM.
\triangle MPE \sim \triangle KTE по двум углам: \angle E — общий, MP \parallel KT \Rightarrow \angle MPE= \angle KTE. S_{KTE}= \frac14S_{MPE}= \frac{68}{4}= 17. S_{MPTK}= 68-17= 51.
Площадь треугольника АВС равна 76, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
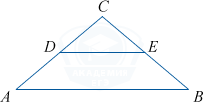
S_{ABED}=S_{ABC}-S_{CDE}. DE — средняя линия, параллельая стороне AB, поэтому D и E — середины сторон.
CD=\frac12CA, CE=\frac12CB, S_{ABC} =\frac12CA\cdot CB\sin C,
S_{CDE}= \frac12CD\cdot CE\sin C= \frac12\cdot\frac12CA\cdot\frac12CB\sin C= \frac14\cdot\frac12CA\cdot CB\sin C= \frac14 S_{ABC}= \frac{76}{4}=19
S_{ABED}= S_{ABC}-S_{CDE}= 76-19=57.
Основания равнобедренной трапеции равны 10 и 90, а её боковые стороны равны 41. Найдите площадь трапеции.
Рассмотрим равнобедренную трапецию ABCD, в которой BC = 10, AD = 90 — основания, AB = CD = 41.
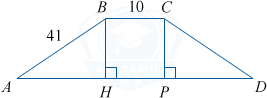
Проведём высоты CP и BH. BCPH — прямоугольник, BC = PH = 10. Прямоугольные треугольники ABH и DCP равны по гипотенузе и катету (AB = CD, BH = CP), тогда AH = PD = (90 - 10) : 2 = 40.
Треугольник ABH прямоугольный, BH = \sqrt{41^2-40^2} = 9.
Площадь трапеции равна S = \frac{BC+AD}{2}\cdot BH= \frac{10+90}{2}\cdot 9= 450.
Основания равнобедренной трапеции равны 15 и 43. Косинус острого угла трапеции равен 0,7. Найдите боковую сторону.
Рассмотрим равнобедренную трапецию ABCD, в которой BC=15, AD=43 — основания, AB=CD.
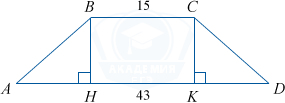
Проведём высоты CK и BH. BCKH — прямоугольник, BC=KH=15. Треугольники ABH и DCK равны по гипотенузе и острому углу, откуда AH=KD=(43-15):2=14. Треугольник ABH прямоугольный, \cos A=\frac{AH}{AB}. Боковая сторона трапеции AB=AH:\cos A=14:0.7=20.
Найдите площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45^{\circ}.
Рассмотрим прямоугольную трапецию ABCD с основаниями BC=16 и AD=22, \angle A=90^{\circ}, \angle D=45^{\circ}. Проведём высоту CH. ABCH — прямоугольник, BC=AH=16, тогда HD=22-16=6.
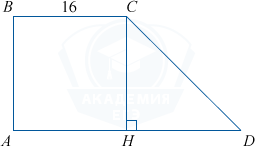
Треугольник CDH прямоугольный и равнобедренный (т.к. \angle CHD=90^{\circ}, \angle HCD=45^{\circ}=\angle D). HD=HC=6.
Площадь трапеции S=\frac{BC+AD}{2}\cdot CH=\frac{16+22}{2}\cdot6=114.
Основания равнобедренной трапеции равны 9 и 53. Тангенс острого угла равен \frac{6}{11}. Найдите высоту трапеции.
Рассмотрим рисунок:
.png)
BK\perp AD и CM\perp AD, тогда AK=MD=\frac{53-9}{2}=22.
\frac{BK}{AK}=tg\angle BAK=\frac{6}{11}, поэтому BK=AK\cdot\frac{6}{11}=22\cdot\frac{6}{11}=12.
Основания прямоугольной трапеции имеют длины 4 и 8. Ее большая сторона с основанием образуют угол равный 45^{\circ}. Найдите площадь трапеции.
.png)
Пусть CH — высота трапеции ABCD. Тогда в прямоугольном треугольнике CHD острый угол CHD = 45^{\circ}. Значит, этот треугольник равнобедренный, то есть CH=DH=AD-BC=8-4=4.
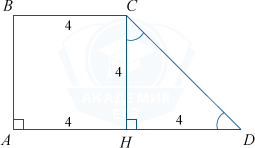
Тогда S_{ABCD}=\frac{AD+BC}{2}\cdot CH=\frac{8+4}{2}\cdot4=24.
Закажите обратный звонок!