Задание №888
Условие
Найдите площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45^{\circ}.
Решение
Рассмотрим прямоугольную трапецию ABCD с основаниями BC=16 и AD=22, \angle A=90^{\circ}, \angle D=45^{\circ}. Проведём высоту CH. ABCH — прямоугольник, BC=AH=16, тогда HD=22-16=6.
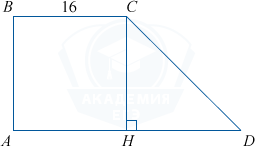
Треугольник CDH прямоугольный и равнобедренный (т.к. \angle CHD=90^{\circ}, \angle HCD=45^{\circ}=\angle D). HD=HC=6.
Площадь трапеции S=\frac{BC+AD}{2}\cdot CH=\frac{16+22}{2}\cdot6=114.
Ответ
114
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.