Задание №1061
Условие
Основания равнобедренной трапеции равны 10 и 90, а её боковые стороны равны 41. Найдите площадь трапеции.
Решение
Рассмотрим равнобедренную трапецию ABCD, в которой BC = 10, AD = 90 — основания, AB = CD = 41.
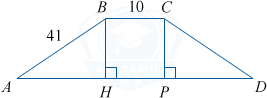
Проведём высоты CP и BH. BCPH — прямоугольник, BC = PH = 10. Прямоугольные треугольники ABH и DCP равны по гипотенузе и катету (AB = CD, BH = CP), тогда AH = PD = (90 - 10) : 2 = 40.
Треугольник ABH прямоугольный, BH = \sqrt{41^2-40^2} = 9.
Площадь трапеции равна S = \frac{BC+AD}{2}\cdot BH= \frac{10+90}{2}\cdot 9= 450.
Ответ
450
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.