Задание №1065
Условие
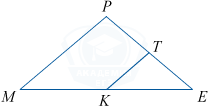
Площадь треугольника МРЕ равна 68, KT — средняя линия, параллельная стороне MP. Найдите площадь трапеции MPTK.
Решение
S_{MPTK}=S_{MPE}-S_{KTE}. KT — средняя линия, параллельная стороне MP, поэтому K и T — середины сторон и ET=\frac12EP, KE=\frac12 EM.
\triangle MPE \sim \triangle KTE по двум углам: \angle E — общий, MP \parallel KT \Rightarrow \angle MPE= \angle KTE. S_{KTE}= \frac14S_{MPE}= \frac{68}{4}= 17. S_{MPTK}= 68-17= 51.
Ответ
51
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.