Задания по теме «Сюжетные задачи из жизни»

а) При n=3 строка ответов состоит из 11 клеток, в каждую из которых записывается 1 или 0. Выясним, каким числом способов можно заполнить эту строку. Первую клетку из 11 можно заполнить 2 способами (записать в неё 1 или 0). Если первая клетка уже заполнена, то вторую клетку также можно заполнить 2 способами. Значит, первые две клетки можно заполнить 4 способами (2\cdot 2=2^2 ). Если первые две клетки уже заполнены, то третью клетку можно опять заполнить 2 способами. Значит, три клетки можно заполнить 8 способами (2^2\cdot 2=2^3 ). Рассуждая аналогично, получаем, что 11 клеток можно заполнить 2^{11} способами, 2^{11}=2048. При n=3 число возможных результатов равно 2048.

б) При n=2 строка ответов состоит из 7 клеток, в каждую из которых записывается 1 или 0. Так как в средней клетке строки уже записана 1, а в симметричные относительно неё клетки записываются одинаковые числа, то для заполнения всех 7 клеток надо заполнить лишь 3 первые клетки. Последние три будут им попарно симметричны относительно средней клетки, и заполняются они одинаково. Из пункта а) следует, что таких возможностей 2^3=8. Число возможных различных «исключительных» результатов при n=2 равно 8.

в) Покажем, что число всех различных одновременно «уникальных» и «проходных» результатов при произвольном значении n равно 4^{n-1}. Так как n > 1, то n=k+1 (k \in \mathbb Z), тогда 4n- 1=4k+3. По условию в средней клетке (её номер 2k+2) содержится 1. Обозначим через m количество единиц в первых 2k+1 клетках, расположенных левее средней клетки. Тогда в этих клетках будет 2k+1 -m нулей. Общее число единиц во всём «исключительном» результате будет равно 2m+1, а общее число нулей равно 2(2k +1-m)=4k -2m+2. По условию для «проходного» результата выполняется неравенство: 2m+1 > 4k-2m+2, 4m > 4k+1, m > k+\frac14 , m \geqslant k+1, так как m является натуральным числом. Заметим также, что m \leqslant 2k+1. При каждом указанном значении m число различных результатов равно C_{2k+1} ^m. Тогда искомое число результатов равно: C_{2k+1} ^{k+1}+C_{2k+1} ^{k+2}+...+C_{2k+1} ^{2k}+C_{2k+1} ^{2k+1}. Известно, что у последовательности биномиальных коэффициентов C_{2k+1} ^0 ,C_{2k+1} ^1 ,...,C_{2k+1} ^{k-1} ,C_{2k+1} ^k ,\! C_{2k+1} ^{k+1} ,C_{2k+1} ^{k+2} ,...,C_{2k+1} ^{2k} ,C_{2k+1} ^{2k+1} , коэффициенты, равноотстоящие от концов, равны. Поэтому сумма C_{2k+1} ^{k+1} +C_{2k+1} ^{k+2} +...+C_{2k+1} ^{2k} +C_{2k+1} ^{2k+1} , равна половине суммы всех коэффициентов. Но сумма всех биномиальных коэффициентов, как известно, равна 2^{2k+1}. Значит, искомая сумма равна \frac{2^{2k+1}}2 =2^{2k}=4^{n-1}.

г) Решим неравенство 4^{n-1} \leqslant 1700. Заметим, что 4^5 =1024 < 1700, а 4^6=4096 > 1700. Поэтому n-1 \leqslant 5, n \leqslant 6. Наибольшее значение n равно 6.

а) 2048; б) 8; в) 4n-1; г) 6.

а) При n=1 строка ответов состоит из 7 клеток, в каждую из которых записывается 1 или 0. Выясним, каким числом способов можно заполнить эту строку. Первую клетку из семи можно заполнить 2 способами (записать в неё 1 или 0). Если первая клетка уже заполнена, то вторую клетку также можно заполнить 2 способами. Значит, первые две клетки можно заполнить 4 способами (2\cdot 2=2^2). Если первые две клетки уже заполнены, то третью клетку можно опять заполнить 2 способами. Значит, три клетки можно заполнить 8 способами (2^2\cdot 2=2^3 ). Рассуждая аналогично, получаем, что 7 клеток можно заполнить 2^7 способами, 2^7=128. Количество всех возможных различных результатов равно 128.

б) При n=2 строка ответов состоит из 11 клеток, в каждую из которых записывается 1 или 0. Так как в средней клетке в указанных карточках уже записана 1, а в симметричные относительно неё клетки записываются одинаковые числа, то для заполнения всех 11 клеток надо заполнить лишь 5 первых клеток. Пять последних будут им попарно симметричны относительно средней клетки, и заполняются они одинаково. Из пункта а) следует, что таких возможностей 2^5=32. Количество всех возможных «особенных» результатов при n=2 равно 32.

в) Покажем, что число всех различных одновременно «особенных» и «удовлетворительных» результатов при произвольном значении n равно 4n. Действительно, по условию в средней клетке (её номер 2n+2) содержится 1. Обозначим через m количество единиц в первых 2n+1 клетках, расположенных левее средней клетки. Тогда в этих клетках будет 2n+1-m нулей. Общее число единиц во всём «особенном» результате будет равно 2m+1, а общее число нулей равно 2(2n+1-m)=4n-2m+2. По условию для «удовлетворительного» результата выполняется неравенство: 2m+1 > 4n-2m+2, 4m > 4n+1, m > n+\frac14 , m\geqslant n+1, так как m является натуральным числом. Заметим также, что m \leqslant 2n+1.

Для решения задачи остаётся посчитать количество всех последовательностей, состоящих из нулей и единиц, в которых единиц больше.

Рассмотрим произвольную последовательность длиной (2n+1), состоящую из нулей и единиц. Всего таких последовательностей 2^{2n}+1 (см. решение пункта а)). Так как число (2n+1) нечётно, то нулей и единиц не может быть поровну, то есть либо нулей больше, либо единиц.

Докажем, что количество последовательностей, в которых единиц больше, равно количеству последовательностей, в которых больше нулей. Для этого каждой последовательности длины (2n+1), в которой преобладают единицы, поставим в соответствие последовательность длины (2n+1) с преобладанием нулей, заменив в исходной последовательности все единицы нулями, а нули — единицами. Например, последовательности 11001 будет соответствовать 00110.

Отсюда количество последовательностей с преобладанием единиц равно \frac{2^{2n+1}}2=4^n.

г) Решим неравенство 4n \leqslant 1500. Заметим, что 4^5=1024 < 1500, а 4^6=4096 > 1500. Значит, n \leqslant 5. Наибольшее значение n равно 5.

а) 128; б) 32; в) 4^n ; г) n=5.

а) Возможно. Пример строится так: достаточно, чтобы из А и Б перешел всего один человек, имеющий показатель Q ниже, чем рейтинг группы А, но выше чем рейтинг группы Б.

Пусть рейтинги участников группы Б были: 1, 1, 1, рейтинги участников группы А были: 5, 8, 8. Из группы А в группу Б перешел человек с рейтингом 5. Рейтинг группы А повысился с 1 до 2, рейтинг группы Б повысился с 7 до 8.

б) Докажем для произвольных групп А и Б, что если при переходе нескольких человек из группы А в группу Б рейтинг обеих групп растет, то:

1) До перехода рейтинг группы А был больше рейтинга группы Б;

2) После перехода рейтинг группы А остается больше рейтинга группы Б.

Введем обозначения:

m — число людей в исходной группе А, A — сумма их показателей;

n — число людей в исходной группе Б, B — сумма их показателей;

k — число перешедших людей, X — сумма их показателей.

По условию, рейтинг обеих групп вырос, то есть \frac{A-x}{m-k}>\frac{A}{m}, \: \frac{B+x}{n+k}>\frac{B}{n}.

Из неравенства \frac{A-X}{m-k}>\frac{A}{m} получаем:

m(A-X)>A(m-k),  mX<Ak,  \frac{A}{m}>\frac{X}{k}, то есть, рейтинг изначальной группы A больше рейтинга группы «перебежчиков». Кроме того, из неравенства mX<Ak можно получить: mX-kX<Ak-kX,  X(m-k)<k(A-X),  \frac{X}{k}<\frac{A-X}{m-k}, то есть рейтинг уменьшенной группы А также больше рейтинга группы «перебежчиков».

Аналогично, из неравенства \frac{B+X}{n+k} > \frac{B}{n} получаем:

n(B+X) > B(n+k),  nX > Bk,  \frac{X}{k} > \frac{B}{n}, то есть, рейтинг изначальной группы Б меньше рейтинга группы «перебежчиков». Кроме того, из неравенства nX > Bk можно получить: nX+kX < Bk+kX,  X(n+k) > k(B+X),  \frac{X}{k} > \frac{B+X}{n+k}, то есть рейтинг увеличенной группы Б также меньше рейтинга группы «перебежчиков».

Таким образом, оба наших вспомогательных утверждения доказаны, ввиду \frac{A}{m} > \frac{X}{k} > \frac{B}{n} и \frac{A-X}{m-k} > \frac{X}{k} > \frac{B+X}{n+k}. Следовательно, одновременное увеличение рейтингов обеих групп возможно лишь при переходах людей в одну сторону (из А в Б) и невозможно при переходе в другую сторону (из Б в А).

в) Расположим по невозрастанию показатели людей в группе А:

a_{1} \geq a_{2} \geq ... \geq a_{10}. Тогда рейтинг группы А до перехода равен \[\frac{a_{1}+a_{2}+...+a_{10}}{10}\], а после перехода он не превосходит a₁ (так как средний рейтинг группы не может превосходить наибольший показатель ее участников). Следовательно, после перехода рейтинг группы А увеличился не более чем на a_{1}-\frac{a_{1}+a_{2}+...+a_{10}}{10}= 0,9a_{1}-\frac{a_{2}+a_{3}+...+a_{10}}{10}. Заметим, что сразу все перешедшие не могут иметь показатель умственных способностей 1, так как в этом случае не произойдет рост рейтинга группы Б. Поэтому a_{2} \geq 2 и a_{2}+a_{3}+...+a_{10} \geq 10. Поэтому при рассматриваемом переходе людей рейтинг группы А растет не более чем на 0,9a_{1}-\frac{a_{2}+a_{3}+...+a_{10}}{10} \leq 0,9 \cdot 9-1=7,1. Значение 7,1 достигается в примере, когда в группе А находятся люди с показателями 9, 2, 1, 1, 1, 1, 1, 1, 1, 1, а в группе Б все имеют показатель, равный 1. В группу Б переходят все из группы А, кроме человека с показателем 9. Рост рейтинга группы А составляет \frac{9}{1}-\frac{19}{10}=7,1.

а) да, б) нет, в) 7,1

а) Так как билет (6;9) является выигрышным, то, согласно стратегии (3), (6\cdot 2; 9\cdot 2) является выигрышным, значит, билет (12;18) является выигрышным.

Так как (6;9) = (3\cdot 2; 3\cdot 3), то, согласно стратегии (3), билет (3\cdot 2\cdot 2; \color{red}{3\cdot 3\cdot 2}) является выигрышным. Аналогично, так как (3\cdot 2; 3\cdot 3) является выигрышным, то (\color{red}{3\cdot 2\cdot 3}; 3\cdot 3\cdot 3) является выигрышным.

Заметим, что выделенные красным числа 3\cdot 3\cdot 2 и 3\cdot 2\cdot 3 равны, поэтому, согласно стратегии (2), билет (3\cdot 2\cdot 2; 3\cdot 3\cdot 3) является выигрышным, то есть (12;27) является выигрышным.

Из предыдущего, согласно стратегии (3), получаем, что (24; \color{red}{54}) является выигрышным. Так как (3\cdot 2; 3\cdot 3) является выигрышным, то (3\cdot 2\cdot 3\cdot 3; 3\cdot 3\cdot 3\cdot 3)является выигрышным, то есть (\color{red}{54}; 81) является выигрышным. Тогда, согласно стратегии (2), билет (24;81) является выигрышным.

б) Билет (3\cdot 2^1; 3\cdot 3^1) является выигрышным по условию. Выше установлено, что билеты (12;27) = (3\cdot 2^2; 3\cdot 3^2) и (24;81) = (3\cdot 2^3; 3\cdot 3^3) также являются выигрышными.

Рассмотрим теперь выигрышный билет (3\cdot 2^3; 3\cdot 3^3). Умножаем числа номера на 2, получим, что билет (3\cdot 2^4; \color{red}{3\cdot 3^3\cdot 2}) является выигрышным.

Так как (3\cdot 2; 3\cdot 3) является выигрышным, то (\color{red}{3\cdot 2\cdot 3^3}; 3\cdot 3\cdot 3^3) является выигрышным. Отсюда, по стратегии (2) получаем, что билет (3\cdot 2^4; 3\cdot 3^4) является выигрышным.

И вообще, если билет (3\cdot 2^s; 3\cdot 3^s), s \in \mathbb{N} является выигрышным, то, умножая числа номера на 2, получаем, что (3\cdot 2^{s+1}; \color{red}{3\cdot 3^s\cdot 2}) является выигрышным. Так как (3\cdot 2; 3\cdot 3) является выигрышным, то, умножая числа этого номера на 3^s, получим, что билет (\color{red}{3\cdot 2\cdot 3^s}; 3\cdot 3\cdot 3^s) является выигрышным.

Отсюда по стратегии (2) получаем, что билет (3\cdot 2^{s+1}; 3\cdot 3^{s+1}) является выигрышным. Тем самым доказано, что билеты с номером (3\cdot 2^k; 3\cdot 3^k) являются выигрышными для любого натурального k.

в) Выше установлено, что билет с номером (3\cdot 2^m; 3\cdot 3^m) является выигрышным. Тогда, умножая числа номера на 3^n, получим, что билет (3\cdot 2^m\cdot 3^n; 3\cdot 3^{m+n}) выигрышный.

Совершенно аналогично убеждаемся, что билет (3\cdot 2^p\cdot 3^q; 3\cdot 3^{p+q}) является выигрышным. Но m+n = p+q по условию, поэтому 3\cdot 3^{p+q} = 3\cdot 3^{m+n}. Пусть 3\cdot 3^{p+q} = A, тогда билеты (3\cdot 2^m\cdot 3^n; A) и (3\cdot 2^p\cdot 3^q; A) являются выигрышными. Применяя сначала стратегию (1), потом стратегию (2), получим, что билет (3\cdot 2^m\cdot 3^n; 3\cdot 2^p\cdot 3^q) является выигрышным.

Что и требовалось доказать.

а) Если бы кресла стояли в ряд, то первое кресло можно было бы выбрать шестью способами, второе — пятью, третье — четырьмя. Всего было бы 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2=720 способов.

Однако за счет поворота каждый способ при таком подсчете считается пять раз, то есть \frac {720}{5}=144 способа.

б) Если представлены кресла четырех видов, то три вида представлены одним креслом, а один вид — двумя. Один вид, представленный двумя креслами, мы можем выбрать шестью способами. Затем из пяти оставшихся выбираем три вида, это можно сделать таким же числом способов, каким можно выбрать два неиспользуемых вида из пяти, то есть \frac{5 \cdot 4}{2}=10 способами.

Значит, существует 60 способов выбрать один вид, представленный двумя креслами, и три вида, представленные одним креслом.

Пусть описанный выше выбор сделан, и у нас уже отобрано 5 кресел. Сначала расставим их в ряд, считая различными. Получим 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120 способов. Теперь учтем то, что один вид повторяется дважды. Получим: \frac{120}{2}=60 способов. Наконец, учтем повороты и получим: \frac{60}{5}=12 способов. Значит, всего 60 \cdot 12=720 способов.

в) Возможны 3 случая.

1) Все кресла различны. Тогда соответствующих способов — 144 (см. пункт а).

2) Три вида представлены одним креслом, а один вид — двумя. Таких способов — 720 (см. пункт б).

3) Один вид кресел представлен на карусели одним креслом, а двум видам соответствует по два кресла. Выбрать один вид, а затем два других можно 60 способами (не учитывая порядок выбора двух последних).

Если бы 5 кресел были различными, то их можно было бы расставить в ряд 5! =120 способами. Учитывая повторяющиеся кресла, получим:

\frac{120}{2 \cdot 2}=30 способов, а учитывая повороты — \frac{30}{5}=6 способов. Всего в этом случае 6 \cdot 60=360 способов.

Общее число способов равно 720+360+144=1224.

а) 144; б) 720; в) 1224.

а) Введем на клетках систему координат.

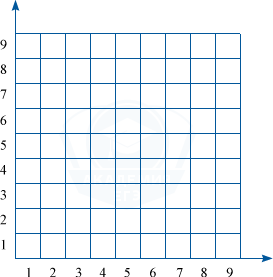
Изначально «Кентавр» стоит в клетке (1;1). Тогда последовательность ходов (1;1) \rightarrow (2;3)\rightarrow (4;2)\rightarrow (2;1) приведет его в клетку (2;1), соседнюю с начальной.

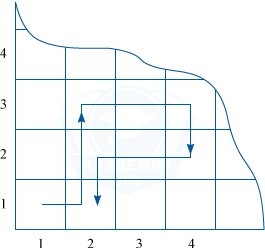
По сути ход «Кентавра» совпадает с ходом обычного шахматного коня.

б) Не может. Если «Кентавр» стоит в клетке (i; j), то после хода он окажется в одной из клеток (i\pm 1; j\pm 3) или (i\pm 3; j\pm 1). Таким образом, сумма координат станет равной одному из чисел i+j-4, i+j-2, i+j+2,i+j+4, то есть изменится на четное число по сравнению с значением i+j. Значит, четность суммы координат клетки, на которой стоит «Кентавр», остается неизменной. Сначала «Кентавр» стоит на клетке (1;1). Следовательно, сумма координат занимаемой клетки всегда будет четной, в то время как соседние с начальной клетки (1;2) и (2;1) имеют нечетную сумму координат.

в) Очевидно, что k\leqslant8, иначе «Кентавр» первым же ходом выскочит за доску. Ясно, что для четных k требуемое невозможно, так как в этом случае «Кентавр» всегда будет оказываться в клетках с черной суммой координат и никогда не сможет попасть ни в клетку (1;2), ни в клетку (2;1). Кроме того, при k>4 после первого хода «Кентавр» окажется либо в клетке (9; k+1), либо в клетке (k+1;9) и следующим ходом вынужден будет вернуться в клетку (1;1), так как 2k+1>9 и, следовательно у него не будет выбора. Тогда все клетки, на которых может побывать «Кентавр», исчерпываются клетками (1;1), (k+1;9) и (9; k+1), то есть в соседней с начальной клетке «Кентавр» никогда не окажется.

Предположим, что k=3. Тогда после первого хода «Кентавр» окажется в клетке (9;4) или (4;9). Будем считать, что он окажется в клетке (9;4), так как второй случай полностью симметричен. Из клетки (9;4) вторым ходом он может либо вернутся в начальную, либо перейти в клетку (1;7), из которой следующим ходом можно лишь вернуться в клетку (9;4). Значит при k=3 «Кентавру» доступны только клетки (1;1), (9;4), (1;7), (4;9), (7;1), и этот случай не подходит.

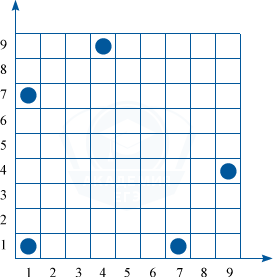
Наконец при k=1 требуемое возможно, что доказывается примером последовательности шагов, приводящих «Кентавра» в соседнюю клетку (1;1)\;\rightarrow\; (2;9)\;\rightarrow\; (3;1)\;\rightarrow\; (4;9)\;\rightarrow\; (5;1)\;\rightarrow\; (6;9)\;\rightarrow\; (7;1)\;\rightarrow\; (8;9)\;\rightarrow\; (9;1)\;\rightarrow\; (1;2)

а) да; б) нет; в) 1.

а) Пусть тестировались трое участников, набравших 20, 48 и 60 баллов. Средний балл не сдавших равен (20+48): 2=34 балла. После прибавления баллы стали 25, 53 и 65. Средний балл несдавших стал равен 25, он понизился.

б) Рассмотрим пример пункта а). Средний бал сдавших стал равен (53+65): 2=59, что меньше среднего балла сдавших до прибавления, который был равен 60.

в) Пусть в тестировании принимало участие N участников, не сдали тест k участников, после добавления баллов не сдали тест p участников.

Пусть a_{1}\leqslant a_{2}\leqslant ...\leqslant a_{N} - баллы участников, тогда a_{k}<50, a_{k+1}\geqslant 50, a_{p}+5<50, a_{p+1}+5\geqslant 50.

Средний балл до добавления:

несдавших \frac{a_1+a_2+...+a_k}{k}=40, сдавших \frac{a_{k+1}+...+a_N}{N-k}=60, всех участников \frac{a_1+a_2+...+a_N}{N}=50. Тогда:

40k+60(N-k)=50N

40k+60N-60k-50N=0

10N=20k

N=2k.

Так как k и N целые, то N делится на 2.

Аналогично после добавления получим:

43p+63(N-p)=55N

20p=8N

2N=5p

N делится на 5.

N делится на 2 и на 5. Значит, N делится на 10.

Пример для 10 участников.

4 плучили по 38 баллов, 1 — 48, 5 — по 60 баллов.

Средний балл, у тех, кто не сдал тест после повышения: (4\cdot 38+48):5=40 баллов.

Средий балл у несдавших после повышения — 43 балла.

Средний балл у сдавших — (48+5+5\cdot 65):6=63 балла.

Условия выполнены.

а) да; б) да; в) 10.