Задания по теме «Прямоугольный треугольник»
Открытый банк заданий по теме прямоугольный треугольник. Задания B6 из ЕГЭ по математике (профильный уровень)
В треугольнике ABC угол C равен 90^{\circ}, BC=8, tg A=0,4. Найдите AC.
Задание №893
Условие
Решение
tg A=\frac{BC}{AC},
\frac{8}{AC}=0,4,
AC=8:0,4=20.
.png)
Ответ
20
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №296
Условие
В треугольнике ABC угол C равен 90^{\circ}, CH — высота, BH=7, \sin A=\frac13. Найдите AB.
Решение
По условию \sin A=\frac13. \angle A=\angle BCH, значит, \sin\angle BCH=\frac13 и \frac{BH}{BC}=\frac13.
BC=3BH=3\cdot7=21.
Высота CH проведена из вершины прямого угла \triangle ABC, поэтому она делит его на два подобных треугольника CBH и ABC.
Из подобия \frac{BH}{BC}=\frac{BC}{BA}, BA=\frac{BC^2}{BH}=\frac{21^2}{7}=63.
Ответ
63
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №290
Условие
В треугольнике ABC\:\angle C=90^{\circ}, CH — высота, BC=14,\, \sin A=0,7. Найдите BH.
Решение
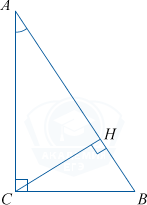
В прямоугольном треугольнике ABC\:\angle A=90^{\circ}-\angle B,\, \sin A=\sin(90^{\circ}-\angle B)=\cos \angle B=0,7.
В \triangle BHC\:\cos\angle B=\frac{BH}{BC}, BH=BC\cdot\cos \angle B=14\cdot0,7=9,8.
Ответ
9,8
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №70
Условие
Треугольник ABC имеет прямой угол C = 90^{\circ}, AC = 12, \cos A=\frac{\sqrt{51}}{10}. Найдите высоту CH.
.png)
Решение
Рассмотрим треугольник ACH. Мы знаем, что косинус угла равен отношению прилежащего катета к гипотенузе, значит:
\cos A = \frac{AH}{AC}
AH=AC\cdot \cos A=12\cdot\frac{\sqrt{51}}{10}
Используя теорему Пифагора, найдем высоту CH:
CH^2=AC^2-AH^2=144-\frac{144 \cdot 51}{100}=\frac{7056}{100}
CH=\sqrt{\frac{7056}{100}}=\frac{84}{10}=8,4
Ответ
8,4
Задание №67
Условие
Треугольник ABC имеет прямой угол C = 90^{\circ}, cos A = 0,41. Найдите sin B.
.png)
Решение
Косинус угла равен отношению прилежащего катета к гипотенузе, т.е. \cos A=\frac{AC}{AB}.
Синус угла равен отношению противолежащего катета к гипотенузе, т.е. \sin B=\frac{AC}{AB}.
В силу данных утверждений, получаем, что sin B = cos A = 0,41
Ответ
0,41
Задание №65
Условие
Треугольник ABC имеет прямой угол C = 90^{\circ}, AC = 5, \cos A = \frac45. Найдите высоту CH.
Решение
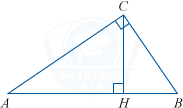
Рассмотрим треугольник ACH. Мы знаем, что косинус угла равен отношениею прилежащего катета к гипотенузе, значит:
\cos A = \frac{AH}{AC}
AH=AC\cdot \cos A=5\cdot\frac{4}{5}=4
Используя теорему Пифагора, найдем высоту CH:
CH^2=AC^2-AH^2=25-16=9
CH=\sqrt{9}=3
Ответ
3