Задание №290
Условие
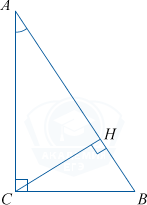
В треугольнике ABC\:\angle C=90^{\circ}, CH — высота, BC=14,\, \sin A=0,7. Найдите BH.
Решение
В прямоугольном треугольнике ABC\:\angle A=90^{\circ}-\angle B,\, \sin A=\sin(90^{\circ}-\angle B)=\cos \angle B=0,7.
В \triangle BHC\:\cos\angle B=\frac{BH}{BC}, BH=BC\cdot\cos \angle B=14\cdot0,7=9,8.
Ответ
9,8
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.