Задания по теме «Куб»
Открытый банк заданий по теме куб. Задания B8 из ЕГЭ по математике (профильный уровень)
При увеличении ребра куба на 3 его площадь поверхности увеличивается на 306. Найдите ребро куба.
Задание №318
Условие
Решение
Поверхность куба состоит из 6 граней, каждая из которых является квадратом, поэтому площадь поверхности куба S=6a^2, где a — ребро куба.
По условию 6(a+3)^2-6a^2=306,
(a+3)^2-a^2=51,
(a+3-a)(a+3+a)=51,
3\cdot(a+3+a)=51,
2a+3=17,
a=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №309
Условие
Во сколько раз увеличится объем куба, если все его ребра увеличить в семь раз?
Решение
Пусть a — ребро исходного куба. Тогда его объем V_1=a^3; После увеличения ребро куба будет равно 7a, а его объем V_2=(7a)^3=343a^3. Тогда \frac{V_2}{V_1}=\frac{343a^3}{a^3}=343.
Ответ
343
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №112
Условие
Диагональ куба равна \sqrt{48}. Найдите объем куба.
Решение
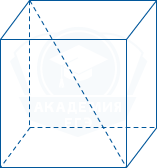
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Так как все измерения куба равны a, то
d^2=a^2+a^2+a^2
48 = 3a^2
a^2=16
a = 4
Зная сторону куба, найдем его объем
V = a^3 = 64
Ответ
64