Открытый банк заданий по теме фигуры на координатной плоскости, точки, векторы. Задания B3 из ЕГЭ по математике (профильный уровень)
Точки O(0; 0), B(15; 4), C(0; 18) и A являются вершинами параллелограмма. Найдите ординату точки A.
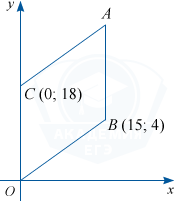
Стороны параллелограмма CO и AB равны и параллельны оси ординат Oy. Значит, ординату точки A можно найти следующим образом: y_a=y_b+AB, при этом AB=OC=18, y_B=4.
Тогда y_A=4+18=22.
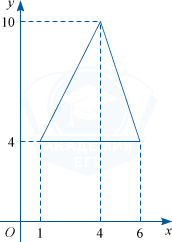
Найдите площадь треугольника, изображенного на координатной плоскости, с вершинами (1; 4), (4; 10), (6; 4).
.png)
Площадь треугольника вычисляется по формуле:
S_{ABC}=\frac12AC\cdot BH
По рисунку видно, что AC=6-1=5,\:BH=10-4=6;
Значит S_{ABC}=\frac{5\cdot 6}{2}=15.
Найдите площадь трапеции, изображенной на координатной плоскости.
.png)
Для нахождения площади трапеции, нужно из площади образовавшегося прямоугольника вычесть площади двух треугольников (см. рис.)
.png)
Площадь треугольника вычисляется по формуле:
S=\frac12ah
где \alpha – длина основания; h – высота треугольника.
Площадь первого треугольника:
S_1=\frac12\cdot3\cdot4=6
Площадь второго треугольника:
S_2=\frac12\cdot3\cdot6=9
Площадь прямоугольника:
S_3=3\cdot8=24
Таким образом, площадь трапеции:
S=S_3-S_1-S_2=24-6-9=9
Найдите площадь трапеции, изображенной на координатной плоскости, с вершинами (1; 1), (10; 1), (7; 8), (2; 8).
.png)
Трапецию можно представить в виде комбинации двух треугольников и прямоугольника. Площадью трапеции является сумма площадей этих фигур.
.png)
Площадь треугольника вычисляется по формуле:
S=\frac12ah
где \alpha – длина основания; h – высота треугольника.
Длина первого треугольника равна 2 − 1 = 1.
Длина второго треугольника: 10 − 7 = 3.
Высоты обоих треугольников: 8 − 1 = 7.
Площадь первого треугольника:
S_1=\frac12\cdot7\cdot1=3,5
Площадь второго треугольника:
S_2=\frac12\cdot7\cdot3=10,5
Площадь прямоугольника:
S_3=7\cdot5=35
Площадь трапеции:
S=S_1+S_2+S_3=3,5+10,5+35=49
Найдите площадь трапеции, изображенной на координатной плоскости.
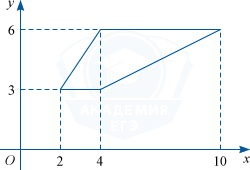
Трапецию можно представить в виде комбинации двух треугольников. Площадью трапеции является сумма площадей этих треугольников.
.png)
Площадь треугольника вычисляется по формуле:
S=\frac12ah
где \alpha – длина основания; h – высота треугольника.
Длина первого треугольника равна 4 − 2 = 2.
Длина второго треугольника: 10 − 4 = 6.
Высота обоих треугольников: 6 − 3 = 3.
Площадь первого треугольника:
S_1=\frac12\cdot3\cdot2=3
Площадь второго треугольника:
S_2=\frac12\cdot3\cdot6=9
Площадь трапеции:
S=S_1+S_2=3+9=12
Закажите обратный звонок!