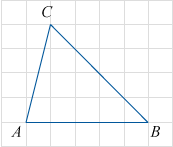
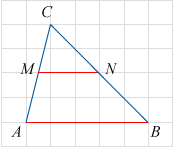
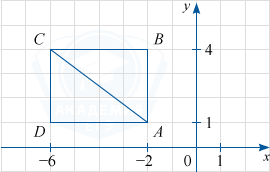
Задания по теме «Геометрические фигуры на плоскости: нахождение длины, площади, угла, координат»
Открытый банк заданий по теме геометрические фигуры на плоскости: нахождение длины, площади, угла, координат. Задания B3 из ЕГЭ по математике (профильный уровень)
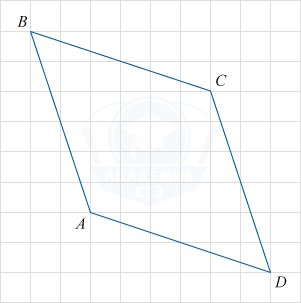
.png)
.png)