Задание №1040
Условие
На клетчатой бумаге с размером клетки \sqrt{10}\times\sqrt{10} изображен четырехугольник ABCD. Найдите его периметр.
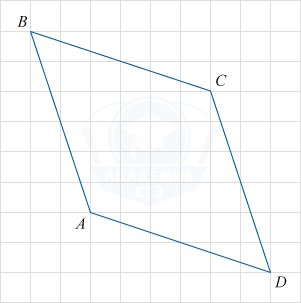
Решение
\triangle BKC = \triangle MDC = \triangle AFD = \triangle ABE по двум катетам, следовательно BC=CD=AB=AD, откуда следует, что ABCD — ромб.
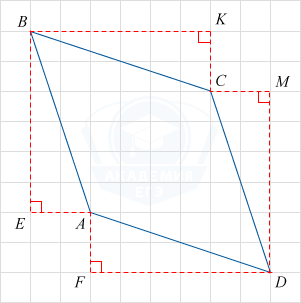
BK=6\sqrt{10}, KC=2\sqrt{10}, BC=\sqrt{BK^2+KC^2}=\sqrt{(6\sqrt{10})^2+(2\sqrt{10})^2}=20.
Пусть P_{ABCD} — периметр ромба ABCD.
P_{ABCD} = 4\cdot BC=4\cdot20=80.
Ответ
80
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Алиса Черная /
Артём Чащин /