Открытый банк заданий по теме фигуры на квадратной решетке. Задания B3 из ЕГЭ по математике (профильный уровень)
На клетчатой бумаге с размером клетки \sqrt{10}\times\sqrt{10} изображен четырехугольник ABCD. Найдите его периметр.
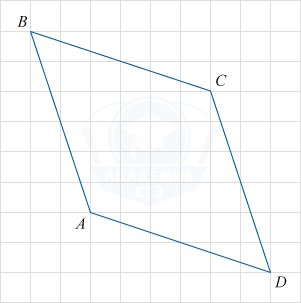
\triangle BKC = \triangle MDC = \triangle AFD = \triangle ABE по двум катетам, следовательно BC=CD=AB=AD, откуда следует, что ABCD — ромб.
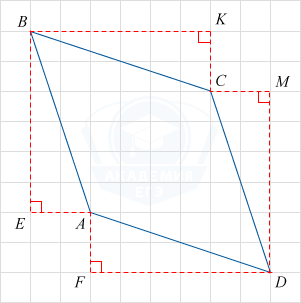
BK=6\sqrt{10}, KC=2\sqrt{10}, BC=\sqrt{BK^2+KC^2}=\sqrt{(6\sqrt{10})^2+(2\sqrt{10})^2}=20.
Пусть P_{ABCD} — периметр ромба ABCD.
P_{ABCD} = 4\cdot BC=4\cdot20=80.
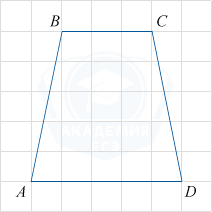
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
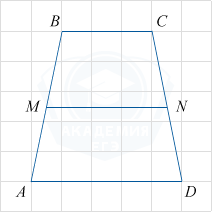
Проведем среднюю линию MN трапеции ABCD. Ее длина равна полусумме оснований трапеции: MN=\frac{AD+BC}{2}. По рисунку AD=5, BC=3, а значит MN=\frac{5+3}{2}=4.
На клетчатой бумаге с размером клетки 1×1 изображен треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
.png)
Построим высоту CH и посчитаем клетки:
.png)
CH = 3.
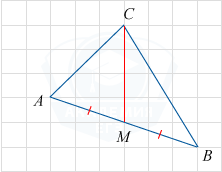
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
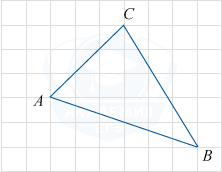
M — середина стороны AB, следовательно, CM — медиана, CM = 4.
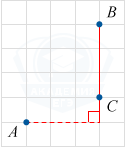
На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
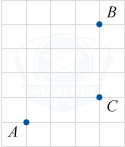
Посчитаем по клеткам расстояние от точки A до прямой BC. Оно равно 3.
На клетчатой бумаге изображён круг площадью 36. Найдите площадь заштрихованного сектора.
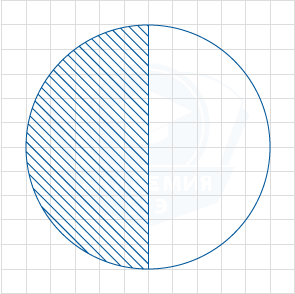
Площадь заштрихованного сектора равна половине площади всего круга, т.е. его площадь равна 0,5\cdot36=18.
На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
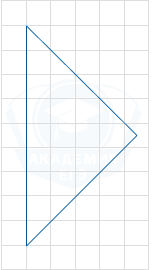
Длина медианы, проведённой к гипотенузе, равна половине гипотенузы. Гипотенуза AB = 9. Медиана CM = 4,5.
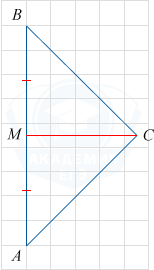
На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB.
Рассмотрим прямоугольный треугольник ABC, в котором катет BC = 5, катет AC = 12. Гипотенузу AB найдём по теореме Пифагора. AB = \sqrt{AC^2+BC^2}=\sqrt{12^2+5^2}=13.
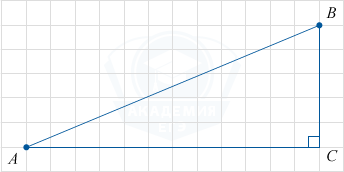
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
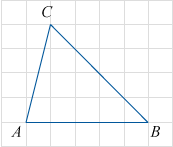
Длина средней линии MN равна половине длины стороны AB, равной 5.
MN=\frac12AB=\frac12\cdot5=2,5
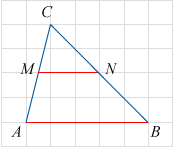
Найдите площадь параллелограмма, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.
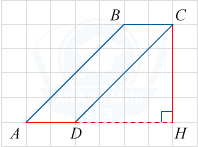
Проведём высоту CH параллелограммаABCD.
S_{ABCD}=AD\cdot CH.
AD=2, CH=4,
S_{ABCD}=2\cdot4=8
Закажите обратный звонок!