Задания по теме «Четырехугольники»
Открытый банк заданий по теме четырехугольники. Задания B3 из ЕГЭ по математике (профильный уровень)
Открытый банк заданий по теме четырехугольники. Задания B3 из ЕГЭ по математике (профильный уровень)
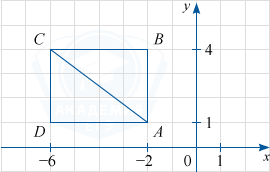
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (-2; 1), (-2; 4), (-6; 1), (-6; 4).
Диагонали прямоугольника равны. Диагональ AC найдём как гипотенузу прямоугольного треугольника ADC с катетами AD=4, CD=3:
AC=\sqrt{AD^2+CD^2}=\sqrt{4^2+3^2}=5
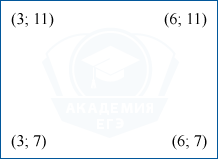
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (3; 7), (3; 11), (6; 7), (6; 11).
У точек (3; 7) и (6; 7) одинаковые ординаты, поэтому длина основания прямоугольника равна 6-3=3. Аналогично, высота прямоугольника равна 11-7=4. Значит, диагональ равна \sqrt{3^2+4^2}=5.
Диагонали AC и BD равнобедренной трапеции ABCD перпендикулярны. Найдите среднюю линию трапеции, если ее высота равна 47.
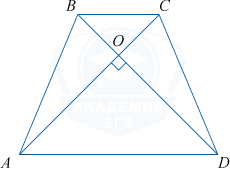
Так как трапеция ABCD равнобедренная, то \triangle AOB = \triangle DOC по стороне и двум прилегающим углам. Тогда \triangle AOD равнобедренный. Так как он еще и прямоугольный, то \angle ADO = 45^{\circ}. Пусть ВН — высота трапеции ABCD. Тогда в прямоугольном \triangle BHD углы при гипотенузе BD равны по 45^{\circ}. Значит, \triangle BHD также равнобедренный, то есть DH=BH=47.
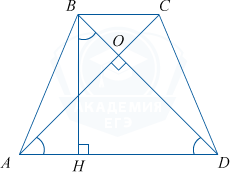
В равнобедренной трапеции DH= BC+AH= BC+\frac{AD-BC}{2}= \frac{2BC+AD-BC}{2}= \frac{BC+AD}{2}. Но DH=47, значит, средняя линия трапеции равна \frac{BC+AD}{2}=47.
Закажите обратный звонок!