Задание №264
Условие
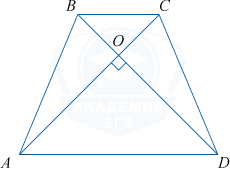
Диагонали AC и BD равнобедренной трапеции ABCD перпендикулярны. Найдите среднюю линию трапеции, если ее высота равна 47.
Решение
Так как трапеция ABCD равнобедренная, то \triangle AOB = \triangle DOC по стороне и двум прилегающим углам. Тогда \triangle AOD равнобедренный. Так как он еще и прямоугольный, то \angle ADO = 45^{\circ}. Пусть ВН — высота трапеции ABCD. Тогда в прямоугольном \triangle BHD углы при гипотенузе BD равны по 45^{\circ}. Значит, \triangle BHD также равнобедренный, то есть DH=BH=47.
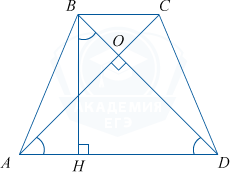
В равнобедренной трапеции DH= BC+AH= BC+\frac{AD-BC}{2}= \frac{2BC+AD-BC}{2}= \frac{BC+AD}{2}. Но DH=47, значит, средняя линия трапеции равна \frac{BC+AD}{2}=47.
Ответ
47
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.