Открытый банк заданий по теме равнобедренный треугольник. Задания B6 из ЕГЭ по математике (профильный уровень)
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30^{\circ}. Боковая сторона треугольника равна 14. Найдите площадь этого треугольника.
.png)
Площадь треугольника можно найти как половину произведения двух его сторон на синус угла между ними. В заданном треугольнике площадь S=\frac12\cdot14\cdot14\cdot\sin30^{\circ}=49.
В треугольнике ABC угол A = 30^{\circ}, AC = BC. Найдите угол C.
.png)
Углы при основании равнобедренного треугольника равны, значит \angle B = \angle A = 30^{\circ}. Зная, что сумма углов треугольника равна 180^{\circ}, найдем искомый угол:
\angle C = 180^{\circ}-2 \cdot 30^{\circ} = 120^{\circ}
В равнобедренном треугольнике ABC стороны AB = BC, AC = 16, CH = 4. Найдите синус угла ACB.
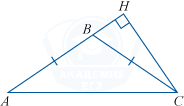
Так как в равнобедренном треугольнике стороны при основании равны, то ∠ACB = ∠CAB. Рассмотрим треугольник AHC. Синус угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе, т.е.:
\sin CAH=\sin ACB=\frac{CH}{AC}=\frac{4}{16}=0,25
Найдите площадь равнобедренного треугольника, если угол, противолежащий основанию, равен 30^{\circ}, а боковая сторона равна 12.
Площадь треугольника равна половине произведения его сторон на синус угла между ними, т.е.:
S = \frac12\cdot a\cdot b\cdot \sin \alpha
Подставим значения и получим:
S = \frac12\cdot 12\cdot 12\cdot \sin 30^{\circ}=36
Закажите обратный звонок!