Задания по теме «Расстояние от точки до плоскости»

а) Плоскости MNK и DBC параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Докажем это. Рассмотрим прямые MN и KM плоскости MNK и прямые BC и DB плоскости DBC.

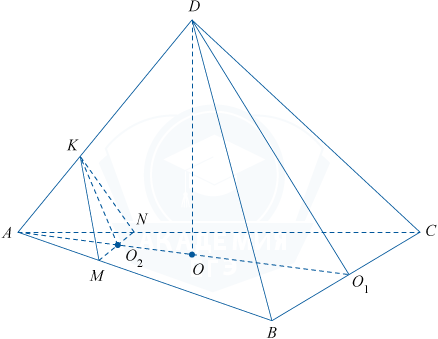
В треугольнике AOD: \angle AOD = 90^\circ и по теореме Пифагора AD=\sqrt{DO^2 +AO^2}.

Найдём AO, используя то, что \bigtriangleup ABC правильный.

AO=\frac{2}{3}AO_1, где AO_1 — высота \bigtriangleup ABC, AO_1 = \frac{a\sqrt{3}}{2}, где a — сторона \bigtriangleup ABC.

AO_1 = \frac{6\sqrt{3} \cdot \sqrt{3}}{2}=9, тогда AO=6, AD=\sqrt{8^2 + 6^2}=10.

1. Так как \frac{AK}{AD}=\frac{5}{2} : 10=\frac{1}{4}, \frac{AM}{AB}=\frac{3\sqrt{3}}{2} : 6\sqrt{3}=\frac{1}{4} и \angle DAB — общий, то \bigtriangleup AKM \sim ADB.

Из подобия следует, что \angle AKM = \angle ADB. Это соответственные углы при прямых KM и BD и секущей AD. Значит KM \parallel BD.

2. Так как \frac{AN}{AC}=\frac{3 \sqrt{3}}{2 \cdot 6 \sqrt{3}}=\frac{1}{4}, \frac{AM}{AB}=\frac{1}{4} и \angle CAB — общий, то \bigtriangleup ANM \sim \bigtriangleup ACB.

Из подобия следует, что \angle ANM = \angle ACB. Эти углы соответственные при прямых MN и BC и секущей AC. Значит, MN \parallel BC.

Вывод: так как две пересекающиеся прямые KM и MN плоскости MNK соответственно параллельны двум пересекающимся прямым BD и BC плоскости DBC, то эти плоскости параллельны — MNK \parallel DBC.

б) Найдём расстояние от точки K до плоскости BDC.

Поскольку плоскость MNK параллельна плоскости DBC, то расстояние от точки K до плоскости DBC равно расстоянию от точки O_2 до плоскости DBC и оно равно длине отрезка O_2 H. Докажем это.

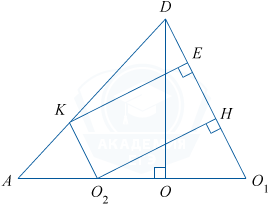
BC \perp AO_1 и BC \perp DO_1 (как высоты треугольников ABC и DBC), значит, BC перпендикулярна плоскости ADO_1, и тогда BC перпендикулярна любой прямой этой плоскости, например, O_2 H. По построению O_2H\perp DO_1, значит, O_2H перпендикулярна двум пересекающимся прямым плоскости BCD, и тогда отрезок O_2 H перпендикулярен плоскости BCD и равен расстоянию от O_2 до плоскости BCD.

В треугольнике O_2HO_1:O_2H=O_{2}O_{1}\sin\angle HO_{1}O_{2}.

O_{2}O_{1}=AO_{1}-AO_{2}.\, \frac{AO_2}{AO_1}=\frac{1}{4}, AO_{2}=\frac{AO_1}{4}=\frac{9}{4}.

O_{2}O_{1}=9-\frac{9}{4}=\frac{27}{4}.

\sin \angle DO_{1}A= \frac{DO}{DO_{1}}= \frac{8}{\sqrt{64+3^2}}= \frac{8}{\sqrt{73}}.

O_2H=\frac{27}{4} \cdot \frac{8}{\sqrt{73}}=\frac{54}{\sqrt{73}}.

\frac{54}{\sqrt{73}}

а) Так как данная призма правильная, то BB_1 \perp ABCD, отсюда BB_1 \perp AC. Поскольку ABCD — квадрат, то AC \perp BD. Таким образом, AC \perp BD и AC \perp BB_1. Так как прямые BD и BB_1 пересекаются, то, согласно признаку перпендикулярности прямой и плоскости, AC \perp BB_1D_1D. Теперь по признаку перпендикулярности плоскостей AD_1C \perp BB_1D_1.

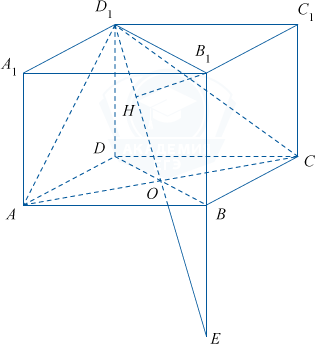
б) Обозначим через О точку пересечения диагоналей AC и BD квадрата ABCD. Плоскости AD_1C и BB_1D_1 пересекаются по прямой OD_1. Пусть B_1H — перпендикуляр, проведенный в плоскости BB_1D_1 к прямой OD_1. Тогда B_1H \perp AD_1C. Пусть E=OD_1 \cap BB_1. Для подобных треугольников D_1B_1E и OBE (равенство соответствующих углов следует из условия BO \parallel B_1D_1) имеем \frac {B_1E}{BE}=\frac{B_1D_1}{BO}=\frac{2}1.

Значит, B_1E=2BE=2 \cdot 6=12. Так как B_1D_1=5\sqrt{2}, то гипотенуза D_1E= \sqrt{B_1E^{2}+B_1D_1^{2}}= \sqrt{12^{2}+(5\sqrt{2})^{2}}= \sqrt{194}. Далее применяем метод площадей в треугольнике D_1B_1E для вычисления высоты B_1H, опущенной на гипотенузу D_1E:

S_{D_1B_1E}=\frac1{2}B_1E \cdot B_1D_1=\frac1{2}D_1E \cdot B_1H; 12 \cdot 5\sqrt{2}=\sqrt{194} \cdot B_1H;

B_1H=\frac{60\sqrt{2}}{\sqrt{194}}=\frac{60}{\sqrt{97}}=\frac{60\sqrt{97}}{97}.

\frac{60\sqrt{97}}{97}

а) Рассмотрим треугольную пирамиду D_1ACD.

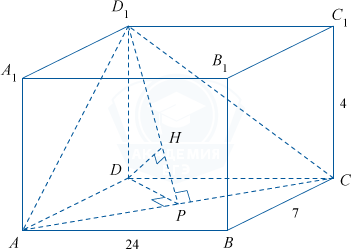
В данной пирамиде расстояние от точки D до плоскости основания ACD_1-DH — равно высоте пирамиды, проведенной из точки D, к основанию ACD_1.

V_{D_1ABC}=\frac1{3}S_{ACD_1} \cdot DH, из этого равенства получаем

DH=\frac{3V_{D_1ACD}}{S_{ACD_1}}.

Рассмотрим пирамиду D_1ABC. Расстояние от точки B до плоскости ACD_1 равно высоте, опущенной из вершины B к основанию ACD_1. Обозначим это расстояние BK. Тогда V_{D_1ABC}=\frac1{3}S_{ACD_1} \cdot BK, из этого получаем BK=\frac{3V_{D_1ABC}}{S_{ACD_1}}.\: Но V_{D_1ACD} = V_{D_1ABC}, так как, если считать в пирамидах основаниямиADC и ABC, то высота D_1D общая и S_{ADC}=S_{ABC} (\bigtriangleup ADC=\bigtriangleup ABC по двум катетам). Значит, BK=DH.

б) Найдем объем пирамиды D_1ACD.

Высота D_1D=4.

S_{ACD}=\frac1{2}AD \cdot DC=\frac1{2} \cdot24 \cdot 7=84.

V=\frac1{3}S_{ACD} \cdot D_1D=\frac1{3} \cdot84 \cdot4=112.

Площадь грани ACD_1 равна \frac1{2}AC \cdot D_1P.

AD_1= \sqrt{AD^{2}+DD_1^{2}}= \sqrt{7^{2}+4^{2}}= \sqrt{65}, \: AC= \sqrt{AB^{2}+BC^{2}}= \sqrt{24^{2}+7^{2}}= 25

Зная, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла, в треугольнике ADC имеем AD^{2}=AC \cdot AP, \: AP=\frac{AD^{2}}{AC}=\frac{7^{2}}{25}=\frac{49}{25}.

В прямоугольном треугольнике AD_1P по теореме Пифагора D_1P^{2}= AD_1^{2}-AP^{2}= 65-\left ( \frac{49}{25} \right )^{2}= \frac{38\:224}{25^{2}}, D_1P=\frac{4\sqrt{2\:389}}{25}.

S_{ACD_1}=\frac1{2} \cdot25 \cdot\frac{4\sqrt{2\:389}}{25}=2\sqrt{2\:389}.

DH=\frac{3V}{S_{ACD_1}}=\frac{3 \cdot112}{2\sqrt{2\:389}}=\frac{168}{\sqrt{2\:389}}.

\frac{168}{\sqrt{2\:389}}

а) В треугольнике BSC проведем высоту BE. Соединим точки B, E и F. \bigtriangleup BEF — искомое сечение.

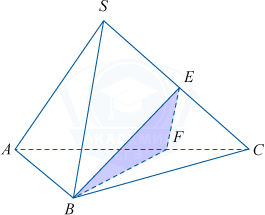
б) 1) Изобразим тетраэдр так, как показано на рисунке ниже:

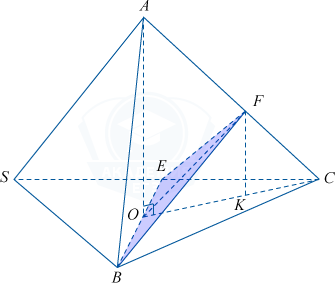
Пусть AO — высота правильного тетраэдра ABCS, AO\perp (BSC). Так как тетраэдр правильный то O — центр описанной окружности \bigtriangleup BCS, CO — ее радиус, CO=\frac{a\sqrt{3}}{3}, где a=12 — сторона правильного треугольника SBC, CO =4\sqrt{3}.

2) \bigtriangleup CAO — прямоугольный, \angle AOC=90^{\circ}. По теореме Пифагора AO=\sqrt{AC^2-CO^2}=\sqrt{144-48}=4\sqrt{6}.

3) Пусть FK\perp CO. Тогда FK \parallel AO, AO\perp (BSC), следовательно, FK\perp (BSC). Значит, FK — искомое расстояние.

4) Заметим, что \bigtriangleup FCK \sim \bigtriangleup AOC по двум углам (\angle FKC=\angle AOC=90^{\circ}, \angle C — общий), тогда \frac{FK}{AO}=\frac{FC}{AC}=\frac{FC}{FC+AF}. Учитывая, что по условию AF=2FC, получаем \ \frac{FK}{AO}=\frac{FC}{FC+2FC}=\frac{1}{3}, FK=\frac{AO}{3}=\frac{4\sqrt{6}}{3}.

\frac{4\sqrt{6}}{3}